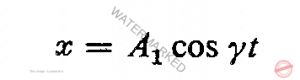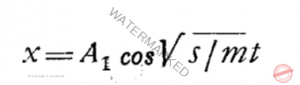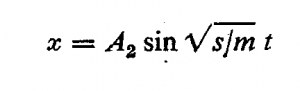مبانی آکوستیک
اصول ارتعاش
بخش اول
آکوستيك به معنای وسیع کلمه تولید، تراگسيل، و دریافت انرژی به صورت ارتعاش در ماده است. اگر اتمها و مولکولهای شاره یا جامد از اوضاع طبیعی خود تغییر مکان یا بند نیروی الاستیك در آن پدیدار می گردد، که مربوط به سختی جسم است؛ و می خواهد جسم را به حالت نخست بازگرداند. این را نیروی برگرداننده گویند. به عنوان مثال می توان نیروی کشش حاصل در فنر کشیده شده، ازدیاد فشار شاره، هنگام تراکم، نیروی برگرداننده يك سیم را هنگامی که دو سر آن ثابت و یکی از نقاط آن در امتداد عمود بر طول سیم کشیده شود نام برد. تأثیر این نیروی الاستيك برگرداننده توأم با خاصیت اینرسی دستگاه، ماده را برای ارتعاش های نوسانی و در نتیجه ترا گسیل موجهای آکوستیکی قابل می سازد.
و برای تولید و انتشار موجهای آکوستیکی، ارتعاش های مختلفی وجود دارند. ارتعاش هایی را که سبب تولید و انتقال موجهای آکوستیکی می شوند بر حسب حدود فرکانسشان به سه نوع طبقه بندی می کنند: ارتعاش های صوتی، که در ایجاد صدا مؤثرند و با گوش شنیده می شوند. حدود فرکانس این نوع ارتعاشها برای گوش عادی بین ۲۰ سیکل بر ثانیه تا ۱۵۰۰۰۰ سیکل بر ثانیه است. ارتعاش های فراصوتی ۴ از فرکانس های ۱۵۰۰۰ سیکل بر ثانیه به بالا، وارتعاش های فروصوتیه، از فرکانس های ۲۰ سیکل بر ثانیه به پايين. مدهای ارتعاشی نیز انواع گوناگونی دارند، از سینوسوئید حاصل از ارتعاش صوت اصلی دیاپازن گرفته تا ارتعاش پیچیده ای که از مالش آرشه روی سیم ویولن به دست می آید، یا ارتعاش درهم برهمی که از نوسانهای غیر متناوب سر وصدا یا انفجار ایجاد می گردد. در مطالعه این قبیل ارتعاشها بهتر است از ساده ترین مد آن، یعنی ارتعاش جیبی، که دارای يك فرکانس است، شروع کنیم.
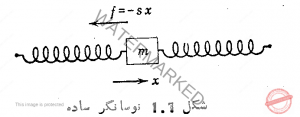
نوسانگرا ساده.
هر گاه جرم m را به يك سر فنری که سر دیگرش به نقطه ای ثابت شده باشد متصل کنیم، و از حال تعادل اندکی در امتداد محور فنز رها سازیم، به ارتعاش در می آید. آزمایش نشان میدهد که فرکانس نوسان آن ثابت می ماند، و تغییر مکان جرم m نسبت به وضع تعادل خود تابع جیبی از زمان است. ارتعاش جیبی از این نوع را ارتعاش هارمونیك ساده می نامند، و دستگاه مرتعش فوق را نوسان کننده ساده می گویند. همچنين آزمایش و محاسبه نشان میدهد که يك جرم هنگامی ارتعاش هارمو نيك ساده خواهد داشت که نیروی برگرداننده فنر که بر اثر سختی فنر پدیدار می شود متناسب با فاصله مرکز جرم از وضع تعادل خود باشد. بیشتر ارتعاش های مورد استفاده در آکوستيک از این نوع یا تقريبا معادل آن هستند؛ مانند ارتعاش دیافراگمهای بلندگو و میکروفون که در فرکانس های کم در اثر ساختمان مخصوص آنها می توان جرمشان را به عنوان يك نقطه متحرك در مرکز فرض کرد، و نوسانهایشان را هارمونيك ساده پنداشت. همچنین بسیاری از دستگاههای مرتعش خصوصیات نوسانگر ساده را دارا می باشند. تنها قانونی که در نوسانگر ساده حکمفرمایی دارد این است که نیروی برگرداننده آن متناسب با فاصله و، با مراعات علامت، با آن مختلف العلامه است. در هر مورد که دامنه ارتعاش به اندازه ای کم باشد که از حد الاستيك فنر تجاوز نکند فرکانس آن به دامنه ارتعاش بستگی ندارد، و ارتعاش به صورت هارمونيك ساده است. ولی اگر دامنه ارتعاش از حد فوق تجاوز کند فرکانس ثابت نمی ماند، وحرکت ارتعاشها هارمونيك ساده نیست؛ و در معادله های آنها تغييراتی حاصل می شود. در مورد صوتهایی که شدتشان عادی است، ارتعاش ازحد الاستيك شاده تجاوز نمی کند، وشرط فوق پایدار می ماند. حتی در صوتهای شدید، مانند صدای حاصل از جمعیت کثیری در يك مسابقه فوتبال، دامنه ارتعاش مولکولهای هوا از يك دهم میلیمتر تجاوز نمی کند، و با این حال هنوز به حد الاستيك هوا نرسیده است. ولی دامنه موج ضربه ای ۴ که در اثر انفجار مواد منفجره ایجاد می گردد ازحد الاستيك هوا تجاوز می کند، و معادله های معمولی آکوستيك برای آنها قابل قبول نیستند. . اينك نوسانگر ساده ای را مطابق شکل 1-1 در نظر میگیریم. نیروی برگرداننده آن را به این صورت می توان نوشت:
که در آن x تغيير مكان جرم m از وضع تعادل، s پایای سختیه به اختصار ، سختی فنر است؛
و علامت منها می رساند که نیروی برگرداننده با تغيير مكان مخالف است. چون مقدار را در معادله عمومی حرکت خطی قرار دهیم
(1.2)
– = m
معادله حرکت نوسانگر به صورت زیر به دست می آید:
که به صورت معادله دیفرانسیل خطی از درجه دوم است، و با روشهای گوناگون می توان آن را حل کرد.
یکی اینکه x را تابع جیبی نسبت به زمان فرض کنیم
چون از این معادله نسبت به زمان مشتق اول ومشتق ثانی بگیریم و در معادله 1.3 
برابر 
می شود. پس یکی از حلهای معادله به این صورت است
همچنین می توان نشان داد که
نیز يك جواب معادله فوق است. پس حل كلی معادله 1.3 دارای دو جمله خواهد بود،
که معمولا به این صورت نوشته می شود
را ثابت فرکانس زاویه ای یا به اختصار فرکانس زاویه ای، یا سرعت زاویه ای می گویند و در موردی که با واژه تنهای فرکانس معرفی شود واژه زاویه ای در آن نهفته است.
فرکانس نوسانگر ساده با 
به وسیله رابطه 
بستگی دارد، و چنین می توان نوشت
چنانکه از رابطه فوق روشن است، هر چه ی، سختی فنر، بیشتر وجرم m کوچکتر باشد فرکانس ارتعاش بیشتر می گردد. این نتیجه ریاضی با مشاهدات فیزیکی تطابق کامل دارد، هرچه فنر شلتر و جرم متصل به آن بزرگتر باشد حرکت ارتعاش ملایمتر یعنی پریود آن، T، بیشتر و فرکانس آن، 
، کمتر خواهد بود.
