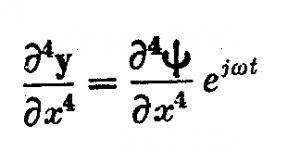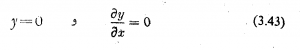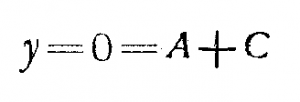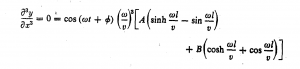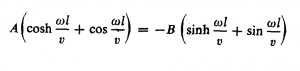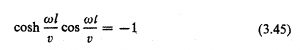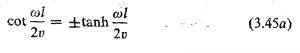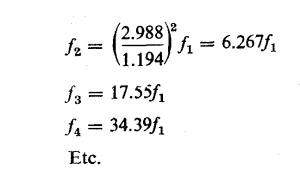مبانی آکوستیک
ارتعاش های میله ها
بخش پنجم
شكل تناوبی حل عمومی معادله انتشار موج عرضی در میله.
فرض کنیم برای حل معادله 3.3.5 جوابی به صورت کلی زیر داشته باشیم
داشته باشیم
که در آن 
، یا به اختصار 
، تابع مختلطی از x و
تابع مختلطی از زمان t باشد .می توان نوشت
اگر مشتقهای بالا را در معادله موج 3.35 قرار دهیم تابع که فقط به x بستگی دارد با معادله دیفرانسیل زیر نموده می شود
اگر سرعتی مانند v، به مقدار
در آن وارد سازیم، به معادله
تبدیل می شود.
اينك فرض می کنیم به صورت مختلط
باشد. اگر آن را در معادله بالا قرار دهیم
بر حسب 
و 
به دست می آید
بنابراین، حل كلی معادله 3.38 به صورت زیر خواهد بود.
که در آن A ، B ، C و D ، پایاهای مختلط دامنه هستند. اگر رابطه بالا را در معادله 3.36 قرار دهیم، تغییر مکان عرضی چنین نوشته می شود
هیچ يك از حلهای چهارگانه فوق انتشار موج را با سرعت ثابت c نمی رساند. مثلا جمله آخر آن به صورت
نماینده انتشار موجی است که با سرعت v به سمت راست پیش می رود، ولی سرعت v چنانکه از معادله 3.37 برمی آید، خود تابعی از فرکانس است، و این می رساند که هر موج با فرکانس معين سرعت خاص دارد. در موج مرکبی که دارای فرکانسهای متعدد باشد، فرکانسهای بالاتر با سرعت بیشتری پیشروی می کنند، و موجهای با فرکانس کمتر عقب می مانند؛ و این امر سبب تغییر شکل موج می گردد. نتیجه آنکه، سرعت ثابتی برای انتشار موج عرضی در میله نمی توان در نظر گرفت؛ و هر فرکانس با سرعت خاص خود، v ، انتشار می یابد، که آن را سرعت فاز گویند. این پدیده شبيه ترا گسیل نور در شیشه است، که ضمن آن فرکانسهای گوناگون، یعنی رنگهای تا به ۲ مرکب نور، با سرعتهای متفاوت سیر می کنند، و پراکند حاصل می شود. بنا بر این، ميله مرتعش را محيط پراکننده ای برای موجهای عرضی می توان تصور کرد
قسمت حقیقی 
در معادلة مختلط 3.39 حل حقیقی معادله انتشار موج عرضی در میله 3.35 است، که با به کار بردن اتحادهای هیپر بوليك و مثلثاتی می توان به دست آورد
و
به کار بردن اتحادهای بالا حل حقیقی معادله موج را به این صورت در می آورد
که در آن A ، B ، C و D پایاهای حقیقی اند و با مقادیر مختلط A ، B ، C و D، ارتباط دارند. رابطه بین آنها مهم نیست زیرا که با بکار بردن شرایط. ابتدایی و مرزی مستقیما از معادله بالا به دست می آیند.
شرایط مرزی
معادله 3.2 دارای چهار پایای اختیاری است، و تعیین آنها چهار شرط مرزی لازم دارد. دو شرط مرزی در يك انتها، و دو شرط مرزی در انتهای دیگر. این شرایط بستگی به چگونگی پایه های میله دارند، که عبارتند از :
(a) انتهای ثابت. اگر انتهای میله محکم به پایه ثابتی متصل شده و بی حرکت بماند تغییر مکان y و ضریب زاویه 
در این نقطه به ازای تمام مقادیر زمان صفراند، و با دو شرط مرزی زیر معرفی می شوند.
(b) انتهای آزاد. در انتهای آزاد، گشتاور و نیروی برشی 
وارد به ميله درسطحی به فاصله بینهایت كوچك از آن هر دو صفر ند و شرایط مرزی در این نقطه با استفاده از معادله های 3.31 و 3.33 با روابط زیر بیان می شوند.
ميله يك سر آزاد.
فرض می کنیم میله در نقطه 
ثابت، و در نقطه 
آزاد باشد. چنین میله را ميله ثابت – آزاد می نامند و به کار بردن شرایط مرزی در نقطه پین پایاهای اختیاری معادله موج روابط زیر را برقرار می سازد.
و
با شرایط بالا معادله موج بدین صورت خلاصه می شود
همچنین به کار بردن شرایط مرزي 
در نقطه بدین روابط منجر می گردد
و
از دو رابطه بالا، رابطه های زیر بين A و B برقرار می شود
و
که به ازای مقادیر معینی از برابر می شوند. برای به دست آوردن فرکانسهای صادق در معادله های بالا، آنها را برهم تقسیم می کنیم و A و B را در آنها حذف می کنیم. با استفاده از رابطه های مثلثاتی 
و 
، مقادیر با رابطه زیر به دست می آیند
با رسم منحنیهای دوتابع 
و 
برحسب 
وتعيين نقاط تقاطع آنها مقادیر به دست می آیند. ولی این راه غیر عملی است، زیرا کسینوس هیپر بوليك به صورت تقریبا اکسپو نانسیل افزایش می یابد، و جز برای مقادیر كوچك آوردن نقاط تقاطع دو منحنی میسر نیست. راه بهتر این است که با استفاده از اتحادهای
معادله 3.45 را به صورت زیر در آوریم
و نقاط تقاطع منحنیهای دو تابع 
و 
را برحسب 
به دست آوریم
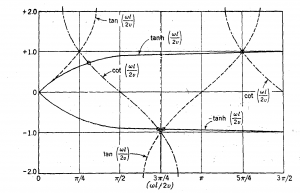
شکل 3.7 منحنیهای دو تابع فوق و محل تقاطع آنها را نشان می دهد، و مدهای ارتعاشی صادق در معادله 3.45 با رابطه زیر داده می شوند.
شكل 3.7 . منحنیهای نماینده – تابعهای تانژانت، کتانژانت، و تانژانت هير بوليك.
مقادیر عددی تانژانت هیپر بوليك به ازای مقادیر بیش از r به واحد نزديك مي شود و ریشه های معادله 
با تقریب زیادی به صورت 
در می آیند که در آن 
است؛ و برابر 
می گردد، و مقادیر 
و 
به دو فرکانس اولی و دومی اختصاص می یابند.
اگر مقدار 
را در معادله 3.46 قرار داده طرفین آن را مربع کنیم، مقادیر فرکانس مدهای ارتعاش پی در پی به دست می آیند
چنانکه ملاحظه می شود، شرایط مرزی شماره مدهای ارتعاشی آزاد را در میله به طول معين محدود می کند، همچنانکه در تارهای مرتعش نیز چنین است، ولی بر خلاف تارهای مرتعش فرکانسهای مدهای ارتعاشی در میله هارمونيك فرکانس اصلی نیستند زیرا از معادلهa 3.47 نشان میدهد که
مشاهده میشود که نخستین فرکانس فرعی اندکی بیش از هارمونيك ششم در تاری به همان فرکانس اصلی است. اگر میله چنان ضربه زده شود که دامنه ارتعاش در بعضی از فرکانسهای فرعی قابل شنیدن باشد، صوت حاصل از میله کیفیت فلزی دارد. ولی، این نتهای فرعی پر فرکانس به زودی از بین می روند، و میله با فرکانس اصلی خود صدا میدهد. چنانکه وقتی دیا پازن را با زدن به عایقی به ارتعاش در آورند، نخست صدای فلزی از آن شنیده می شود، و بعد با فرکانس اصلی خود تن خالص ارتعاش آن ادامه می یابد.
بدین جهت میله ها را به عنوان مولد فرکانسهای استانده در بخش فرکانس و در فیلترهای الکتریکی با فرکانس کم به کار می برند. فرکانسهای اصلی این میله ها را می توان با تغيير ضخامت و یا با تغییر طول تنظیم کرد. یادآوری می کنیم که در میله های يكسر آزاد با مضاعف ساختن طول، فرکانس آن ربع میشود.
چگونگی توزیع نقاط گره در این گونه میله ها مانند تارهای مرتعش نیست. یعنی فاصله دو گره پیاپی ثابت و به میزان 
نمی باشد، بلکه فاصله های بین گره ها نامنظم است. بعلاوه سه نوع نقطه گری در آنها وجود دارد. در انتهای ثابت میله يك گره موجود است که در آن 
و 
و آن را نوع یکم می گویند. در نوع دوم نقطه های گرهی با و 
معرفی می شوند. این نقطه های راگره های حقیقی نامند، و در نقطه های عطف میله 
موجود هستند. فاصله بین این نقطه های تقریبا برابر است. نوع سوم آخرین نقطه گرهی نزديك به انتهای آزاد میله است. در این نقطه ولی نقطه عطف 
نزديك این نقطه نیست، بلکه از آن اندکی دور است. از طرف دیگر، دامنه ارتعاش در نقطه های شکم به يك اندازه نیست، و دامنه ارتعاش انتهای آزاد از همه بیشتر است.
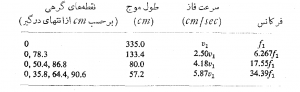
جدول 3.1 مشخصات ارتعاش عرضی میله ای به طول cm100 را نشان می دهد، که يك انتهای آن در 
x ثابت و انتهای دیگر در 
آزاد است؛ و در آن نسبت فرکانسهای پیاپی به فرکانس اصلی، و نسبت سرعتهای فاز پیاپی نسبت به سرعت اصلی و طول موج درهر فرکانس و اوضاع نقطه های گرهی نموده شده است. چنانکه ملاحظه می شود، افزایش سرعت فاز بر حسب فركانس در آن کاملا نمایان است. یاد آوری می کنیم که طول موج در این فرکانسها معمولا دو برابر فاصله بین دو گره پیاپی نیست، ولی از فرکانس فرعی سوم فاصله بین گره ها 
(
)یعنی تقریبا برابر است.
جدول 3.1 مشخصات ارتعاش عرضي ميله يک سر آزاد
