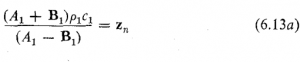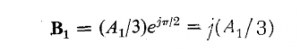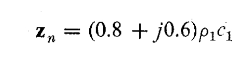مبانی آکوستیک
تراگسیل موج
بخش دوم بازتاب از سطح جامد؛ تا بش عمودی. بازتاب موجهای تخت در يك شاره که از برخورد به يك جامد ايجاد گردد قدری پیچیده تر از بازتابی است که از برخورد به يك شاره ایجاد می شود. به منظور محدود ساختن بررسی بازتاب از يك جامد از تجزیه و تحلیل موج تختی که وارد جامد می شود صرف نظر می کنیم. در عوض رفتار این موج را با پارامتر
امپدانس آکوستیکی ویژه عمودی جامد ، مشخص می کنیم. برابر نسبت فشار آکوستیکی وارد بر سطح جامد به سرعت شاره عمود بر سطح جامد است. از آنجا که ممکن است فشار آکوستیکی با سرعت شاره در سطح جامد همیشه همفاز نباشند امپدانس آکوستیکی ویژه عمودی ممکن است مختلط باشد و در نتیجه
که 
مؤلفه مقاوم و 
مؤلفه واکنشی آن است. اينك فرض می کنیم شاره محیط II در شكل 6.1 به وسيله محيط جامدی جایگزین شده باشد. شرایط مرزی پیوستگی فشار و پیوستگی سرعت ذره ای در 0=x که در بند 6.2 جداگانه به کار رفت، در این مورد به صورت شرط پیوستگی نسبت آنها یعنی
در 0=x در می آید. اگر مقادیر فشار و سرعت ذره ای را در 0=x از معادله های 6.1 ، 6.2 و 6.5 در معادله ی بالا قرار دهیم به این صورت در می آید
با حل کردن معادله 6.13a برای 
خواهیم داشت
یا با قرار دادن مقدار از معادله 6.12
باید توجه کرد که هنگامی که حقیقی باشد، معادله 6.14 با معادله 6.7 معادل می شود. اگر حقیقی نباشد مختلط خواهد بود، و در نتیجه موج بازتاب در مرز ممکن است از موج تابش به میزانی بین 0 تا ° 180 جلو یا عقب باشد. با استخراج مقدار طرف راست معادله 
خواهيم داشت
را که رابطه ای است برای به دست آوردن مقدار دامنه فشار باز تاب. در این حالت ضریب توان صوتی بازتاب چنین خواهد شد
ضریب توان صوتی قراگسیل را می توان از این معادله به دست آورد
معادله ی بالا بیانی از پایدار بودن انرژی آکوستیکی است، بدین معنی که مجموع توانهای بازتاب و تراگسيل باید برابر توان تابشی گردد. پس
در بسیاری از حالتها، موج ترا گسیل در جامد به زودی کاهش می یابد و انرژی آن جذب محیط می گردد. در نتیجه، ضریبا معادله ی 6.17 را غالباً 
ضریب جذب توان صوتی سطح برای تابش عمودی موجها، می گیرند. اينك حالتی را در نظر میگیریم که در آن بازتاب موج از سطوح جامدات سخت وغير متخلخل مانند فولاد، شیشه، سیمان، و غیره رخ دهد. هر گاه محیط این مواد را غير محدود یا به میزانی محدود فرض کنیم که سطح موج لااقل به مساحت چند طول موج در آن پیشروی کند، سه نوع موج الاستيك در آن مواد منتشر می شود که شامل موجهای تخت طولی و برشی هستند. در يك جامد ایزوتروپا که دارای سطح مقطع وسیعی عمود بر امتداد انتشار موج باشد، سرعت حجمی یا سرعت سطحی موجهای طولی چنین است .
که در آن B و G به ترتیب مدولهای حجمی و برشی جامد هستند. مقادیر سرعت حجمی c و همچنين امپدانس مشخص 
برای جامدهای مختلف در جدول I ضمیمه آورده شده است. باید متذکر شد که سرعت حجمی c در هر ماده از سرعت موجهای طولی در میله های نازك از همان ماده که در فصل سوم شرح آن گذشت بیشتر است. بنابراین در معادله های بالا اگر به جای ، مقادیر عددی امپدانس مشخص حجمی حساب شده در مواد جامد مندرج در جدول را قرار دهیم، می توان معادله های بالا را برای بحث بازتاب وترا گسیل موجها در سطوح آن مواد به کار برد . در مواردی که محیط جامد بسیار نازك يا قابل انعطاف باشد چنانکه تمام آن هنگام برخورد موج ما نند پوسته و ورق نازک به ارتعاش در آید، مقدار را نمی توان برابر مربوط به سرعت حجمی قرار داد. در این حالت اینگونه صفحات دارای امپدانس آکوستیکی ویژه عمودی هستند که از حاصل تقسیم فشار آکوستیکی وارد بر آن سطوح بر سرعت ارتعاش آنها به دست می آید و با روشهایی مانند روشی که در پوسته واداشته در بند 4.8 به کار بردیم می توان به دست آورد. بالاخره در موردهایی که مواد جامد متخلخل باشند مانند سفال آکوستیکی، پشم معدنی، آجرهای متخلخل، نمد و غیره. تأثير فشار آکوستیکی بر آنها تنها تراكم الاستیکی جامد نیست، بلکه سبب حرکت رفت و آمدی شاره همراه آن می گردد. در اینگونه مواد امپدانس آکوستیکی ویژه عمودی در سطح برخورد موج، دارای مؤلفه مقاوم و مؤلفه واکنشی است که هر دوی آنها معمولا به فرکانس بستگی دارند، و همچنین عوامل دیگری مانند ضخامت، تخلخل و چگالی نیز در آنها مؤثر است، و می توان برای بررسی به مأخذ زیر مراجعه کرد. تشکیل موجهای ایستاده. هنگامی که موج از يك سطح تخت مرزی در شاره بازتاب می کند موجهای ایستاده در شاره ایجاد می شوند. اگر دامنه ثابت موج بازتاب مختلط باشد می توان با همان روشی که در بند 6.2 استفاده شد ، نشان داد که 
موج ایستاده چنین است
که در آن 
يك زاوية فاز است و با رابطه زیر تعیین می شود
این زاویه نشان میدهد که فشار بازتاب در سطح جامد نسبت به فشار تابش چه مقدار جلو يا عقب است. ایجاد موجهای ایستاده اندازه گیری دامنه فشار موج تابش را مشکل می سازد. بدین سبب در این گونه موردها اندازه گیری در هوا را در اتاقهای مخصوصی به نام اتاقهای بی پز واك و اندازه گیری در آب را در محفظه های بی پژواک انجام میدهند که در آنها دیواره های برخورد موج، جاذب، کامل است و موجهای بازتاب از آنها بسیار ناچیز. برعکس ایجاد موجهای ایستاده در محاسبه ، امپدانس آکوستیکی ویژه عمودی سطح، راهی به دست می دهد که همان روشی است که برای اندازه گیری امپدانس انتهائي مجهول خط انتقال انرژی بر حسب امپدانس خط، به کار برده می شود. اگر مقدار و فاز دامنه فشار بازتاب را بر حسب دامنه 
اندازه گیری کنند و در معادله 
بنهند برحسب 
امپدانس مشخص شاره محاسبه می شود. مقدار بر حسب با اندازه گیری نسبت دامنه فشار موج ایستاده در يك شكم به دامنه فشار آن در يك نقطه گرهی امکان پذیر است، و آن را با علامت SWR نشان می دهند.
این معادله را می توان بر حسب
چنین به دست آورد
بالاخره برای اندازه گیری فاز وضع اولین شکم یا اولین گره را نسبت به سطح بازتاب تعيين می کنند. چنانکه از معادله 6.19 هویداست، نقاط گرهی در مواضعی هستند که 
برابر واحد شود و نخستین گره در فاصله ای از سطح به مقدار x قرار دارد که در رابطه 
صادق باشد و با تعيين تجربی x می توان را محاسبه کرد.
با روش بالا می توان را محاسبه کرد. مثلا فرض کنیم در موردی از تشکیل موج ایستاده،
و اولین گره به فاصله 3.8 طول موج از سطح بازتاب باشد، یعنی
علامت منفی می رساند که مختصات نقاط واقع بر سطح بازتاب صفر و جهت مثبت و در جهت پیشروی موج تا بش است. اگر مقدار x را در معادله ی 6.22 قرار دهیم محاسبه می شود
و چون را در معادله 6.21 قرار دهیم مقدار برابر 1/3 می شود و دامنه ی مختلط فشار موج بازتاب بدین مقدار به دست می آید
که اگر آن را در معادله 6.13a بنهیم چنین نتیجه می شود
در عمل برای سهولت از جدولی به نام جدول اسمیت استفاده می شود که با مشخص بودن SWR و وضع اولين گره مجاور صفحه باز تاب ، مقادير
و 
در آن خوانده میشود و احتیاجی به محاسبه بالا نیست
