مبانی آکوستیک
جذب موج های صوتی در شاره ها
بخش اول پیشگفتار. در فصلهای گذسته در باره اتلاف انرژی صوتی مطلبی بیان نکردیم. در بعضی مواقع اتلاف به قدری با کندی انجام می گیرد که ممکن است آن را نادیده گرفت. با این همه در آخر عمل، تمام انرژی صوتی تنزل پیدا می کند و به شکلی از انرژی گرمایی در می آید. علت این اتلاف را می توان به دو قسمت عمده دسته بندی کرد. قسمت نخست مربوط به اتلاف انرژی صوتی در درون محیط یاشاره ای است که هنگام انتقال صوت در آن پیدا می شود. قسمت دوم مربوط به خصوصیتهای دیواره هایی است که شاره را محدود می سازند. اتلاف مربوط به قسمت نخست وقتی قابل ملاحظه است که حجم شاره در مقایسه با حدودی که آن را احاطه کرده اند نسبتا بزرگی باشد؛ مانند وقتی موج های صوتی در جو یا در سطح اقیانوسها یا در لوله تهویه مطبوع که خیلی گشاد باشد، یا در سالن بسیار بزرگی منتشر می گردند. این اتلاف را به سه علت می توان نسبت داد، که عبارتند از اتلاف براثر چسبناکی، اتلاف براثر هدایت گرمایی، واتلاف براثر مبادله های مولکولی انرژی. اتلاف مربوط به چسبناکی وقتی پیدا می شود که قسمتهای مختلفی از محیط نسبت به یکدیگر دارای حرکت باشند. چون هنگام انتشار صوت در شاره در آن تراکم و انبساط صورت می گیرد، این اتلاف حاصل می گردد. هنگامی که معادله های اساسی انتشار موج های آکوستیکی را می نوشتیم یکی از فرضهای اساسی ما این بود که تغییرات فشار، که توأم با انبساط و تراکم موج های صوتی است، بطور بیدر روا صورت می گیرند. این فرض مستلزم این است که دما تغییر کند. بنابراین وقتی شاره در حال ارتعاش است گرما از قسمت متراکم که دمای آن بیشتر است به سمت قسمت منبسط مجاور که دمایش کمتر است جاری می گردد، و در نتیجه این انتقال گرما، فشار شاره به سمت تعادل می گراید، و این پدیده به تدریج دامنه موجها را در حين انتشار در محیط کاهش می دهد. سرانجام اتلاف انرژی آکوستیکی که توأم با تغییرات ساختمانی مولکولهای محیط است بواسطة محدود بودن زمانی است که لازم است مصرف شود تا این تغییرات حاصل گردند. مثلا وقتی پریود موج های آکوستیکی قابل مقایسه باشد یا زمانی که لازم است تا قسمتی از انرژی شاری متراکم به انرژی داخلی تبدیل گردیده و صرف ارتعاشهای مولکولی شود؛ در این صورت چون در موقع انبساط شاره در برگشت قسمتی از این انرژی به شاره منبسط تأخير دست می دهد، این تأخير سبب می گردد که فشار درون شاره به تدریج رو به تعادل گذارد، و در نتیجه دامنه ارتعاشهای موج های آکوستیکی کاهش پذیرد. در فصل گذشته هنگامی که در باره موج های صوتی بحث می کردیم امکان داشت که شاره انتقال دهنده صوت را محیط پیوسته ای فرض کنیم که دارای چند خاصیت ماکروسکوپی از قبیل فشار، چگالی، تراکم پذیری، گرمای ویژه، دما، و غیره باشد؛ بدون آنکه ساختمان مولکولی و جزئیات دیگر آن محیط را در نظر بگیریم. در سال 1845، استوکس توانست با چنین روشی نخستین نظریه مورد قبول را در باره ساز و کار تنكش موج های صوتی پیشنهاد کند. در سال 1868 کیر شهوفه یکی دیگر از خواص ماکروسکوپی را که عبارت باشد از خاصیت هدایت مورد استفاده قرار داد، و به روش دیگری علت جذب صوت را در شاره بيان کرد. این دو نوع سازو کار را معمولا سازو کار نوع كلاسيك جذب صوت در شاره می نامند. با وجود این در این اواخر هر قدر روش اندازه گیری جذب صوت در شازهها دقیقتر می گشت به همان اندازه روشنتر می گردید که توضیحات سابق در باره علل جذب صوت در شاره، که از طریق استفاده از طریق ماکروسکوپی بیان می گردیده قانع کننده نیستند. در نتیجه لازم شد که از طریق میکروسکوپی به شاره نگاه کنیم، به این معنی که برای یافتن توضیح قانع کننده تری در باره جذب صوت در شاره ها بعضی از پدیده های درونی از قبیل انرژی همگیری را که در داخل و بین مولکولها وجود دارند در نظر بگیریم. ساز و کارهای اخیر را معمولا جذب مولكولی صوت یا جذب صوت در نتیجه و اهلش»؛ یا بطور اختصار جذب مولکولی با جذب و اهلشی می نامند. چنانچه کسب اطلاعات بیشتری نسبت به آنچه در این فصل بیان می شود در باره جذب صوت مورد نظر باشد توصیه می شود به منابعی که در پایین صفحه بعد داده شد . اما اتلاف انرژی مربوط به دیواره های شاره وقتی اهمیت پیدا می کند که حجم شارهای که صوت در آن انتشار می یابد نسبت به سطوح دیواره هایی که آن را محدود می سازند کوچک باشد؛ مانند لوله تهویه ای که باريك باشد و به دیواره های آن مواد جاذب صوت چسبانیده باشند؛ یا هنگامی که در يك اتاق كوچك صحبت کنیم. در این موارد اتلاف انرژی مربوط به دیوار قابل ملاحظه است. در باره جذب صوت که در جدار اتاق ها صورت می گیرد در فصل مربوط به آكوستيك ساختمانی با ذکر جزئیات آن بحث خواهیم کرد. تأخير فاز بین فشار و تراکم. از نظر پدیده شناسی می توان گفت جذب انرژی صوتی در شاره ها توأم با تأخیر زمانی است که تراکم (s) نسبت به فشار آکوستیکی متغیر (p) دارد. می توان ثابت کرد که این تأخیر مربوط است به يك زمان مشخص یا زمان و اهلش که لازم است برای اینکه (1) استرسهای چسبناکی که همیشه با سرعت نسبی ذرات همراهند گرایش به مساوی کردن سرعتها کنند، (۲) گرما از قسمت متراکم که دارای دمای بیشتر است به قسمت منبسط که دارای دمای کمتر است هدایت شود، (۳) تغییر انرژی مولکولی به وقوع پیوندد. بطور دقیقتر می توان گفت که زمان واهلش عبارت از مدتی است که طول می کشد تا عملی که در حال انجام است در پیشرفت خود به 
مقدار تعادل خود برسد. وقتی فشار و تراکم همیشه با یکدیگر همفاز باشند. هیچ گونه اتلافی در انرژی موج های صوتی روی نمی دهد، مانند حالتی که برای نوشتن معادله ی 4.5b فرض کرده ایم، که در آن کلام 
بود. اما اگر تراکم نسبت به فشار تأخير فاز داشته باشد می توان ثابت کرد که در طول هر يك سيكل تغيير فشار مقداری کار به شاره که در مسیر انتقال صوت قرار گرفته داده می شود. این کار فیزیکی که به خرج انرژی موج های آکوستیکی انجام می گیرد صرف زیادشدن دما و انرژی گرمایی شاره می گردد. می توان طرز عمل بالا را به آسانی با مشاهده نمودار PV شكل 3.1 ميجسم کرد. کاری که به شاره داده شده، یعنی W عبارت است از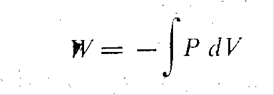 
و مقدار آن به وسيله سطحی که در زیر منحنی PV قرار دارد نمایانده می شود. اگر همیشه فشار و تراکم همفاز باشند کاری که شاره هنگام تراکم گرفته و با منحنی ABC نموده شده برابر با کاری است که شاره هنگام انبساط برگشت داده و با منحنى CBA نموده می شود. از آنجا که در این سیکل هیچ مقدار کاری مبادله نگردیده، انرژی موج های آکوستیکی هم 
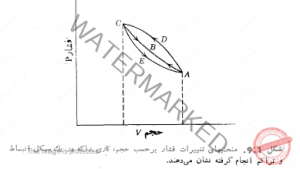تلف نشده است، و در نتیجه دامنه موجها تنکیده نمی گردد. اما اگر تراکم و نسبت به تغییر فشار p تأخير فاز داشته باشد ممکن است شاخه نمایش تراکم بامنحنی ADC وشاخه نمایش انبساط با منحنی CEA نموده شود. در این صورت سطح محصور بين حلقه ADCEA نمایش کار خالصی است که در طول يك سیکل به خرج انرژی موج های آکوستیکی به شاره داده شده است، این اتلاف انرژی موجب کم شدن دامنه فشار موج های صوتی است، زیرا طبق رابطه 5.33b چگالی انرژی موج های صوتی متناسب است با مربع دامنه فشار بنابراین برای اینکه جمله های مربوط به اتلاف را در معادله کلی موجها وارد سازیم لازم است معادله 5.4b را چنان تغییر دهیم که تراکم نسبت به کم و زیاد شدن فشار آکوستیکی تأخیر داشته باشد. تجربه نشان داده که معادله زیر که به وسیله استوکس پیشنهاد شده برای ادای مقصود سودمندتر است 
در این رابطه R عبارت است از نوعی ضریب چسبناکی مؤثر که ما بعدا در قسمتهای مختلف این فصل به تفصیل در باره آن بحث خواهیم کرد. برای اثبات اینکه قبول این معادله سبب می شود که فشار نسبت به تراکم تقدم فاز داشته باشد فرض کنیم فشار متناوبی به معادله 
در شاره فعالیت داشته باشد. اگر رابطه 
را برای تغییرات تراكم بپذیریم، چون آن را در رابطه 9.1 ببریم خواهیم داشت 
معادله بالا نشان میدهد که تراکم نسبت به فشار به اندازه زاویه 
تأخیر فاز دارد، چنانکه 
یاد آوری می گردد، تا آنجا که به آشفتگیهای متناوب فشار مربوط است معادله 9.2 نشان میدهد که می توان اتلاف را در معادله موجها وارد کرد؛ به شرطی که معادله 5.4b را دوباره به شکل زير بنویسیم 
‘c سرعت مختلطی است که با رابطه زیر داده می شود 
برای اینکه معنی معادله 9.1 را بهتر تجسم کنیم فرض کنیم در زمان t=0 یک مقدار فشار اضافی ثابت 
به شاره در حال سکون وارد می سازیم. اگر این شرط اولیه را در حل عمومی معادله دیفرانسیلی که در رابطه 9.1 داده شده به کار بریم خواهیم داشت 
البته خواننده توجه خواهد کرد که این راه حل همان است که در مورد به دست آوردن جریان الکتریسیته با واردساختن يك ولتاژ ثابت 
به دو سر مداری که مقاومت و خودا لقا در آن بطور متوالی قرار گرفته به کار رفته است. هر گاه بعد از آنکه تراکم به آخرین مقدار خود یعنی 
رسید را حذف کنیم، تراکم نیز بر طبق معادله زیر به صفر بر می گردد 
در شكل 9.2 منحنیهایی که معادله های 9.5 و 9.5a را نمایش می دهند رسم گردیده اند. چنانکه دیده می شود، در هر دو حالت تراکم با فوریت از تغییرات فشار پیروی نمی کند، بلکه نسبت به آن تاخیر دارد؛ چنانکه تا رسیدن به اندازه آخرین مقدار خود به اندازه 
واهلش داشته است. این زمان را زمان و اهلش می نامیم، و مشابه است با ثابت زمانی 
که در معادله های مدارهای الکتریکی مشابه با معادله های 9.7 و 9.5 پیدا می شود.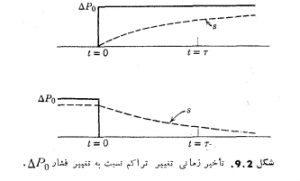 
اگر معادله 9.4 را دوباره بر حسب زمان و اهلش بنویسیم خواهیم داشت 
