مبانی آکوستیک
جذب موج های صوتی در شاره ها
بخش دوم جذب مربوط به چسبناکی در موج های تخت. اکنون بعنوان ذکر مقدمه ای نسبتا آسان در باره ساز و کار بسیار پیچیده جذب صوت ابتدا موضوع تنكش موج های تخت صوتی را در اثر خاصیت چسبناکی باشرح بعضی از جزئیات آن بررسی می کنیم. هر گاه معادله 9.1 و معادله پیوستگی 5.3a ، يعني ![]() و معادله نیرو (5.8)، يعني
و معادله نیرو (5.8)، يعني ![]() ، را طوری با هم ترکیب کنیم که sوp حذف شوند خواهیم داشت
، را طوری با هم ترکیب کنیم که sوp حذف شوند خواهیم داشت ![]() معادله بالا کیفیت تنكش موج های تخت را از طريق تحلیلی بیان می دارد. در بخش گذشته یاد آور شدیم که اتلاف انرژی موج های متناوب را می توان به حساب آورد به شرط آنکه به جای سرعت حقیقی c مقدار مختلط ‘c را به کار بریم که به وسیله معادله 9.4 و 9.4a داده شده است. پس، معادله ی 9.7 برای موج های تنکیده را به صورت مختلط زیر می توان نوشت
معادله بالا کیفیت تنكش موج های تخت را از طريق تحلیلی بیان می دارد. در بخش گذشته یاد آور شدیم که اتلاف انرژی موج های متناوب را می توان به حساب آورد به شرط آنکه به جای سرعت حقیقی c مقدار مختلط ‘c را به کار بریم که به وسیله معادله 9.4 و 9.4a داده شده است. پس، معادله ی 9.7 برای موج های تنکیده را به صورت مختلط زیر می توان نوشت ![]() حل هريك از این دو معادله را می توان برای بحث در باره جذب موج های صوتی به کار برد. برای اینکه همان نوع اعمالی را که در مورد انتشار موج های الكتروما نيتيك در درون دی الکتریکها و همچنین در باره موج های ولتاژ در خطهای ترأگسیل به کار بردیم در اینجا نیز به کار بریم، بسیار سودمند است که همان روشهایی را که در معادله های آنها به کار بردیم در اینجا مورد استفاده قرار دهیم. بنا بر این فرض کنیم که حل دوره ای معادله 9.7a به صورت زیر باشد
حل هريك از این دو معادله را می توان برای بحث در باره جذب موج های صوتی به کار برد. برای اینکه همان نوع اعمالی را که در مورد انتشار موج های الكتروما نيتيك در درون دی الکتریکها و همچنین در باره موج های ولتاژ در خطهای ترأگسیل به کار بردیم در اینجا نیز به کار بریم، بسیار سودمند است که همان روشهایی را که در معادله های آنها به کار بردیم در اینجا مورد استفاده قرار دهیم. بنا بر این فرض کنیم که حل دوره ای معادله 9.7a به صورت زیر باشد ![]() که در آن
که در آن  را پایای مختلط طول موج می نامند، و می توان آن را بر حسب مقدار حقیقی و انگاری به شکل زیر نوشته
را پایای مختلط طول موج می نامند، و می توان آن را بر حسب مقدار حقیقی و انگاری به شکل زیر نوشته ![]() وقتی این مقدار
وقتی این مقدار ![]() را در معادله 4.8 بگذاریم، خواهیم داشت
را در معادله 4.8 بگذاریم، خواهیم داشت ![]() شکل معادله بالا مشابه است با شکل معادله 5.11 که برای موج های تحت ناميرا به دست آورده ایم، به استثنای اینکه در این معادله دامنه جابجایی بر طبق ضريب
شکل معادله بالا مشابه است با شکل معادله 5.11 که برای موج های تحت ناميرا به دست آورده ایم، به استثنای اینکه در این معادله دامنه جابجایی بر طبق ضريب ![]() با زیادشدن فاصله تنکیده می شود. برای
با زیادشدن فاصله تنکیده می شود. برای ![]() و k می توان مقدارهای صریح به دست آورد؛ بدينطریق که
و k می توان مقدارهای صریح به دست آورد؛ بدينطریق که ![]() و
و ![]() را با گذاشتن معادله های 9.10 و 9.44 در معادله 9.9 از معادله اخير حذف کنیم. نتیجه چنین است
را با گذاشتن معادله های 9.10 و 9.44 در معادله 9.9 از معادله اخير حذف کنیم. نتیجه چنین است ![]() وقتی قسمتهای حقیقی وانگاری طرفین معادله بالا را به ترتیب با هم متساوی بگذاریم، دو معادله به شکل زیر به دست می آیند
وقتی قسمتهای حقیقی وانگاری طرفین معادله بالا را به ترتیب با هم متساوی بگذاریم، دو معادله به شکل زیر به دست می آیند 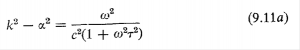 و
و ![]() اگر k را بین دو معادله بالا حذف کنیم می توان ثابت کرد که
اگر k را بین دو معادله بالا حذف کنیم می توان ثابت کرد که ![]() در بیشتر شاره ها زمان واهلش
در بیشتر شاره ها زمان واهلش ![]() به اندازه ای کوچک است که حتی برای فرکانسهایی در حدود مگاسیکل حاصلضرب
به اندازه ای کوچک است که حتی برای فرکانسهایی در حدود مگاسیکل حاصلضرب ![]() آن می شود. پس وقتی این نام مساوی صدق کند معادله پیچیده 9.12 ساده می شود و به صورت زیر در می آید
آن می شود. پس وقتی این نام مساوی صدق کند معادله پیچیده 9.12 ساده می شود و به صورت زیر در می آید  هر گاه به جای
هر گاه به جای ![]() مقدار آن یعنی
مقدار آن یعنی ![]() را بگذاریم، چنین می شود
را بگذاریم، چنین می شود ![]() از مشاهده رابطه بالا آشکار می گردد که اگر R تابع فرکانس نباشد پایای تنکش
از مشاهده رابطه بالا آشکار می گردد که اگر R تابع فرکانس نباشد پایای تنکش ![]() مستقيمة متناسب می شود با مربع فرکانس. در بسیاری از آبگو نها و گازها شرط
مستقيمة متناسب می شود با مربع فرکانس. در بسیاری از آبگو نها و گازها شرط ![]() در فاصله زیادی از فرکانسها مشاهده گردیده است، و از اینرو عادت شده که دانسته های تجربی در باره جذب صوت را به شکل
در فاصله زیادی از فرکانسها مشاهده گردیده است، و از اینرو عادت شده که دانسته های تجربی در باره جذب صوت را به شکل ![]() a یا به شکل کمیتی معادل با آن بر حسب فرکانس رسم کنند. وقتی رسم منحنی بدین ترتیب تهیه گردید هر نوع انحرافی که نسبت به خط مستقیم افقی پیدا شود می تواند نمایش مقدار انحراف نتیجههای آزمایشی از نظریه گفته شده در بالا باشد. . همچنین ممکن است به را میان معادله های 9.11a و 9.11b حذف کرد، و بدین طريق معادله ای برای k دست آورد. جمله حاصل، دیگر به شکل ساده
a یا به شکل کمیتی معادل با آن بر حسب فرکانس رسم کنند. وقتی رسم منحنی بدین ترتیب تهیه گردید هر نوع انحرافی که نسبت به خط مستقیم افقی پیدا شود می تواند نمایش مقدار انحراف نتیجههای آزمایشی از نظریه گفته شده در بالا باشد. . همچنین ممکن است به را میان معادله های 9.11a و 9.11b حذف کرد، و بدین طريق معادله ای برای k دست آورد. جمله حاصل، دیگر به شکل ساده ![]() نیست. از آنجا که من همیشه برابر است با حاصلضرب
نیست. از آنجا که من همیشه برابر است با حاصلضرب ![]() در فرکانس، خواه جذب صوت صورت بگیرد یا نگیرد، تغيير k را می توان به تغيير سرعت نسبت داد. این سرعت تغییر یافته را که با حرف و نمایش می دهند سرعت فاز می نامند و آن را به وسیله معادله زير تعریف می کنند
در فرکانس، خواه جذب صوت صورت بگیرد یا نگیرد، تغيير k را می توان به تغيير سرعت نسبت داد. این سرعت تغییر یافته را که با حرف و نمایش می دهند سرعت فاز می نامند و آن را به وسیله معادله زير تعریف می کنند ![]() وقتی با حذف بين معادله های 9.11a و 9.11b برای رابطه ای به دست آمد آن را در معادله 9.13 می بریم تا معادله زير حاصل گردد
وقتی با حذف بين معادله های 9.11a و 9.11b برای رابطه ای به دست آمد آن را در معادله 9.13 می بریم تا معادله زير حاصل گردد ![]() برای فرکانسهای کم که شرط
برای فرکانسهای کم که شرط ![]() محقق باشد معادله بالا ساده می گردد و به شکل زیر در می آید
محقق باشد معادله بالا ساده می گردد و به شکل زیر در می آید  بستگی سرعت فاز به فرکانس که در رابطه بالا مشاهده می شود، می رساند که واهلش هوجهای صوتی که با خواص چسبناکی محیط همراه است نه تنها موجب تنكش دامنه صوت می شود، بلکه موجب پراکنده در سرعت انتشار موجها نیز می گردد. برای اینکه به بینیم چه موقع شرط آسان کننده
بستگی سرعت فاز به فرکانس که در رابطه بالا مشاهده می شود، می رساند که واهلش هوجهای صوتی که با خواص چسبناکی محیط همراه است نه تنها موجب تنكش دامنه صوت می شود، بلکه موجب پراکنده در سرعت انتشار موجها نیز می گردد. برای اینکه به بینیم چه موقع شرط آسان کننده ![]() قابل استفاده است باید درباره ی ماهیت پایای R پژوهش کنیم. اگر معادله 9.7 را مستقیما به كمك معادله های اساسی هیدرودیناميكا به دست آوریم خواهیم داشت
قابل استفاده است باید درباره ی ماهیت پایای R پژوهش کنیم. اگر معادله 9.7 را مستقیما به كمك معادله های اساسی هیدرودیناميكا به دست آوریم خواهیم داشت ![]() x ضريب طولی چسبناکی است و
x ضريب طولی چسبناکی است و ![]() بیشتر ضریب برشی چسبناکی نامیده می شود. چون هیچ گونه روش مستقیمی برای اندازه گیری x وجود نداشت، استوکس فرض کرد که هر گاه تراکم يکنواختی ازهمه طرف بر شاره وارد شود شاره هیچ نوع عکس العملی مربوط به چسبناکی نشان نخواهد داد. از آنجا که از لحاظ نظری ثابت می شود که ضریب حجمی چسبناکی
بیشتر ضریب برشی چسبناکی نامیده می شود. چون هیچ گونه روش مستقیمی برای اندازه گیری x وجود نداشت، استوکس فرض کرد که هر گاه تراکم يکنواختی ازهمه طرف بر شاره وارد شود شاره هیچ نوع عکس العملی مربوط به چسبناکی نشان نخواهد داد. از آنجا که از لحاظ نظری ثابت می شود که ضریب حجمی چسبناکی ![]() که با تراکم يکنواخت همراه است، باید به وسیله رابطة
که با تراکم يکنواخت همراه است، باید به وسیله رابطة ![]() و بیان گردد؛ بنابراین لازمۀ فرض بالا یعنی
و بیان گردد؛ بنابراین لازمۀ فرض بالا یعنی ![]() این است که
این است که ![]() باشد. وقتی این مقدار نظری x را در معادله 9.15 ببریم خواهیم داشت .
باشد. وقتی این مقدار نظری x را در معادله 9.15 ببریم خواهیم داشت .  چنانکه بعد در همین فصل خواهیم دیده، دلیلی در دست هست که موجب می شود بپذیریم برخی آبگو نها، بویژه آب، دارای ضریب چسبناکی محو نشدنی هستند. اما در حال حاضر فرض كلاسيك استوکس را می پذیریم و معادله 9.15a را به کار می بریم. سرانجام وقتی که مقدار
چنانکه بعد در همین فصل خواهیم دیده، دلیلی در دست هست که موجب می شود بپذیریم برخی آبگو نها، بویژه آب، دارای ضریب چسبناکی محو نشدنی هستند. اما در حال حاضر فرض كلاسيك استوکس را می پذیریم و معادله 9.15a را به کار می بریم. سرانجام وقتی که مقدار ![]() را در معادله 9.6 ببریم می شود
را در معادله 9.6 ببریم می شود ![]() اگر عددهای مناسبی را که در جدول ضميمه I برای هوای ℃20 موجود هستند در معادله بالا بگذاریم خواهیم داشت
اگر عددهای مناسبی را که در جدول ضميمه I برای هوای ℃20 موجود هستند در معادله بالا بگذاریم خواهیم داشت 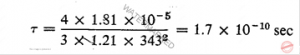 همچنين، عددهای مناسب مربوط به آب را℃20 که در رابطه بالا بگذاریم می شود
همچنين، عددهای مناسب مربوط به آب را℃20 که در رابطه بالا بگذاریم می شود ![]() در هر دو حالت به اندازه ای کوچک است که رابطه
در هر دو حالت به اندازه ای کوچک است که رابطه ![]() و همیشه برای تمام فرکانسها برقرار است. فقط در باره موج های فراصوتی در صورتی که فرکانس آنها بسیار زیاد باشد و در آبگون بسیار غلیظ انتشار یابند می توان پیشبینی کرد که رابطه ساده کننده
و همیشه برای تمام فرکانسها برقرار است. فقط در باره موج های فراصوتی در صورتی که فرکانس آنها بسیار زیاد باشد و در آبگون بسیار غلیظ انتشار یابند می توان پیشبینی کرد که رابطه ساده کننده ![]() دیگر در باره آنها قابل قبول نیست. بنابراین می توانیم فرض کنیم که در همه آبگو نها، مگر آبگو في که بسیار چسبناك باشد، اثر چسبناکی بر موج های آکوستیکی به نوعی است که سرعت انتشار را تابع فرکانس نمی سازد؛ و به علاوه پایای تنکش برابر است با
دیگر در باره آنها قابل قبول نیست. بنابراین می توانیم فرض کنیم که در همه آبگو نها، مگر آبگو في که بسیار چسبناك باشد، اثر چسبناکی بر موج های آکوستیکی به نوعی است که سرعت انتشار را تابع فرکانس نمی سازد؛ و به علاوه پایای تنکش برابر است با  معمولا تنكش دامنه جابجایی ذرات و نیز فشار آکوستیکی و غیره را بر حسب نپر بیان می کنند، که واحد لگاریتم طبیعی است و متناظر است با مقدار کوچک شدن دامنه برای رسیدن به
معمولا تنكش دامنه جابجایی ذرات و نیز فشار آکوستیکی و غیره را بر حسب نپر بیان می کنند، که واحد لگاریتم طبیعی است و متناظر است با مقدار کوچک شدن دامنه برای رسیدن به ![]() مقدار اولیه با مقدار مأخذ. چنانکه در رابطه 9.8a دیدیم ، موج های تخت مستقيمة بأضریب
مقدار اولیه با مقدار مأخذ. چنانکه در رابطه 9.8a دیدیم ، موج های تخت مستقيمة بأضریب ![]() تنکیده می شوند، و حاصلضرب
تنکیده می شوند، و حاصلضرب ![]() باید دارای دیمانسيون
باید دارای دیمانسيون ![]() باشد. این مطلب می رساند که ديما نسبون عبارت است از نپر برمتر. بعلاوه چون شدت موج تخت متناسب است با مربع دامنه ارتعاش، بنا بر این شدت نپر باید بر طبق رابطه
باشد. این مطلب می رساند که ديما نسبون عبارت است از نپر برمتر. بعلاوه چون شدت موج تخت متناسب است با مربع دامنه ارتعاش، بنا بر این شدت نپر باید بر طبق رابطه ![]() با مسافت تغییر کند. در نتیجه تغییر تراز شدت موج های تنکیده بر حسب دسی بل (db) با رابطه زير داده می شود
با مسافت تغییر کند. در نتیجه تغییر تراز شدت موج های تنکیده بر حسب دسی بل (db) با رابطه زير داده می شود 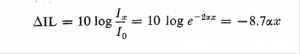 پس، می توانیم بگوییم که 8.7a میزان کاهش فضایی تراز شدت بر حسب
پس، می توانیم بگوییم که 8.7a میزان کاهش فضایی تراز شدت بر حسب ![]() است. همچنین می توانیم آن را اندازه کاهش مساوی با همین مقدار در تراز فشار بدانیم.
است. همچنین می توانیم آن را اندازه کاهش مساوی با همین مقدار در تراز فشار بدانیم.



