مبانی آکوستیک
بلندگوها
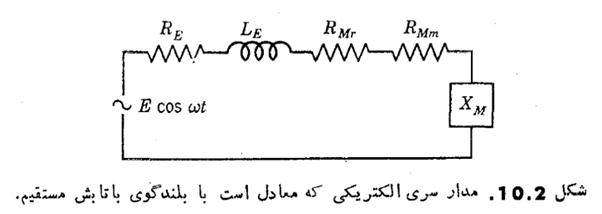
بخش دوم در کار تجزیه و تحلیل بلندگوهای با تابش مستقیم با در مورد تراگذارهای الكترو آکوستیکی از نوع دیگر بسیار مناسب است که به جای سیستم امپدانس واقعی مکانیکی سیستم حرکتی الکتریکی را قرار دهیم. مثلا جریانهای الکتریکی را که در پیچك بلندگوی سابق بر اثر وارد کردن يك ولتاژ برقرار می شود می توان به كمك مدار شکل 10.2 به دست آورد.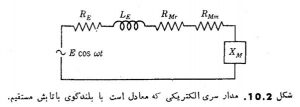 
عنصر های حرکتی 
، 
و 
این مدار با موجه ساختن معادلة مختلط به دست آمده اند. مثلا مؤلفه واکنش عبارت است از 
و مؤلفه مقاومتی کلی 
چنین است 
از مؤلفه مقاومت کلی RM فقط قسمت 
مربوط به انتقال انرژی الکتریکی به انرژی آکوستیکی است. باقیمانده یعنی 
مربوط است به انرژیی که برای خم کردن مخروط بلندگو و پایه های چین دار آن به مصرف می رسد. چون کارآیی الکترو آکوستيك مربوط به بلندگو ( 
) باید مساوی باشد با کارآیی مدار معادل الکتریکی آن، پس 
وقتی که عبارتهای و را که به ترتیب با معادله های 10.13a و 10.13b داده شده اند در رابطه بالا بگذاریم کارآیی به صورت زیر در می آید 
که در آن 
وقتی که جریان متناوب 
را به مدار پیچك صوتی وارد کنیم انرژی آکوستیکی که از بلندگو منتشر می شود بر حسب وات خواهد بود 
و این توانی است که در قسمت مربوط به مدار الکتریکی معادل پخش شده است. از طرف دیگر وقتی ولتاژ متناوب 
را به طرفین پیچك صوتی متصل سازیم مقدار شدت جریان از رابطه زیر به دست می آید 
عبارت است از جمع کل امپدانس الکتریکی در داده که شامل امپدانس باز داشته ( 
) مربوط به پيچك صوتی است و امپدانس حرکتی ( 
) که مربوط است به حرکت پیچش صوتی. در نتیجه رابطه 
بازداد؛ صوتی بر حسب وات را در صورتی که ولتاژ معلومی مانند E به طرفين پيچك صوتی اتصال یافته باشد، به دست می دهد. باید در نظر داشت که نماد های I و E که در معادله های بالا به کار رفته اند هر کدام عبارتند از ریشه دوم متوسط مربعات جریان و ولتا، چنانکه در معادله های نظریه مدارهای الکتریکی نیز به همین معنی به کار می روند. باملاحظه رابطه 10.17 آشکار می شود که اضافه کردن 
یا 
یا E، همچنین کم کردن 
و سبب می گردد که انرژی آکوستیکی باز داده بلندگو افزایش یابد. معادله 10.14a به طریق مشابھی نشان میدهد که اضافه کردن یکی از دو مقدار و یا R کارآیی را زیاد می کند، در صورتی که اگر 
یا 
یا را زیاد کنیم کارآیی کم می شود. اگر لازم باشد توان بازداده آکوستیکی که از توان معين در داده الکتریکی به دست می آید مستقل از فرکانس باشد، باید معادله 10.14a مر بوط به کار آیی نیز تابع فرکانس نباشد. چون دو مقدار و متعلق به این معادله پیچیده هر دو تابع فرکانس اند، بجز برای نوار باریکی از فرکانسها حصول چنین شرطی دشوار است. همچنین باید در نظر گرفت که هرگاه دامنه ثابت جریان در داده I را در معادله 10.15 بگذاریم، یا دامنه ثابت ولتاژ در داده E را در معادله 10.17 به کار بریم با همین اشکال روبرو می گردیم.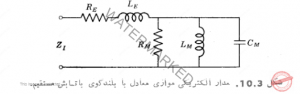 
مدار الکتریکی شکل 10.2 یکی از مدارهای الکتریکی است که ممکن است برای نشان دادن معادل الکتریکی بلندگوی دینامیکی ساده با تابش مستقیم استعمال شود. شکل 10.3 یکی دیگر از این گونه مدارهاست. قابل قبول بودن این مدار وقتی ظاهر می شود که می بینیم امپدانس حرکتی که بوسیله معادله 10.11 داده شده دارای مقدار ماکسیمم 
برای فرکانس رزونانس مکانیکی و است، که با رابطه زیر داده شود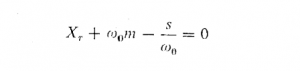 
این رفتار از مختصات سه عنصر RM و 
و 
است، به شرطی که مانند شکل 10.3 نسبت به یکدیگر بطور موازی قرار گرفته باشند. وقتی آنها را موازی بگذاریم مقدار امپدانس الکتریکی ZM می شود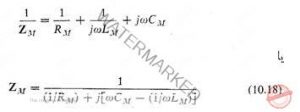 
چون معادله بالا را که ZM را به دست می دهد، با معادله 10.11 مقایسه کنیم می بینم این دو معادله موقعی با هم معادلند که رابطه های زیر برقرار باشند 
به کار بردن مدار موازی از نوع شکل 10.3 جهت پیدا کردن معادله هایی که بتوانند برای کارآیی و بازداد؛ آکوستیکی به کار بروند اصولا ما را به همان معادله هایی می رساند که سابقا برای مدارهای سری بوسیله شكل 10.2 به دست آورده ایم، از اینرو آنها را تکرار نمی کنیم . ولی باید متوجه بود که در مدار معادل موازی عنصر مقاومت حرکتی که بوسیله رابطه 10.19 داده شده با در مدار معادل سری، که با رابطه 10.13 داده شده ، مساوی نیست، مگر در فرکانس رزونانس 
.
