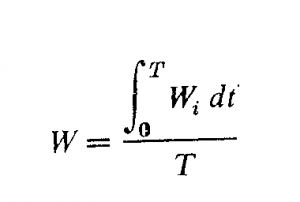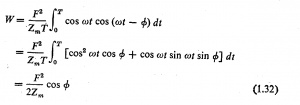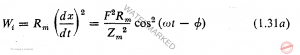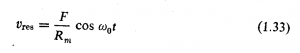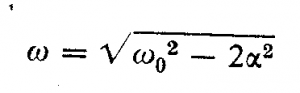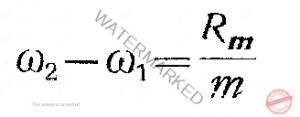مبانی آکوستیک
ارتعاش صدا
بخش هفتم رابطه های توان. توان لحظه ای به حسب وات که به وسیله نیروی راننده به دستگاه وارد می شود برابر حاصلضرب نیروی راننده لحظه ای در سرعت لحظه ای است
باید دانست که توان لحظه ای 
قسمت حقیقی حاصلضرب نیروی راننده مختلط 
و سرعت مختلط v نیست. در بسیاری از موارد توان متوسط W که به دستگاه داده می شود وضع دستگاه را بهتر از توان لحظه ای مشخص می سازد. توان متوسط برابر نسبت مقدار کار داده شده در يك نوسان کامل بر زمان يك نوسان کامل است، یعنی
اگر را از معادله 31.1 در رابطه بالا قرار دهیم W محاسبه می شود.
چنانکه ملاحظه می شود، توان مکانیکی متوسط مشابه توان الکتریکی در مداری شامل مقاومت، خودالقا، و خازن است که بصورت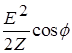 
می باشد (E نیروی محرك الکتریکی ماکسیم). هر گاه به جای F، مقدار ماکسیمم نیرو، مقدار مؤثر آن، 
و به جای E مقدار نیروی محرك الکتریکی ماکسیم، مقدار مؤثر آن، 
را به کار بریم، مضرب 2/1 حذف می شود، و توانهای مکانیکی و الکتریکی با مقادیر مؤثر به صورت های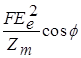 
و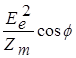 
در می آیند. 
را در توان مکانیکی ضریب توان مکانیکی می نامند، همچنانکه در توان الکتریکی آن را ضریب توان الکتریکی می نامند. چون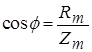 
است، بنابراین معادله 32. ا را به این صورت هم می توان نوشت:
که مستقیما از محاسبه کار انجام داده شده در برابر مقاومت مکانیکی، 
، نیز بدست می آید. توان لحظه ای را از این نظر به این صورت می نویسیم:
اگر متوسط این توان را در يك پريود به دست آوریم، معادله 1.32a به دست می آید. بنابراین، می توان گفت که در حالت پایدار دامنه و فاز نوسانگر طوری با یکدیگر تنظیم می شوند که توان متوسط نیروی راننده آن برابر توان متوسط نیروی اصطكاك باشد. توان متوسط هنگامی به مقدار ماکسیمم خود می رسد که راكتانس مکانیکی 
صفر شود. از معادله 1.32 روشن می شود که فرکانس مربوط به 
برابر 
است، بطوریکه 
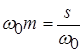است و در این حالت 
ماکسیمم خواهد بود؛ زیرا برابر واحد و 
می نیمم و برابر است. فرکانس رزونانس مکانیکی. فرکانس رزونانس مکانیکی هنگامی به دست می آید که راكتانس برابر صفر باشد، یعنی در این حالت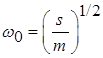 
است. در این فرکانس نیروی راننده ماکسیمم توان را به دستگاه می رساند، و مقدار آن برابر فركانس آزاد دستگاه بدون میرایی است، چنانکه در2-1 شرح آن گذشت. در این فرکانس امپدانس مکانیکی مینیمم و برابر مقاومت مکانیکی است 
و مقداری است حقیقی. همچنین دامنه سرعت در این فرکانس ماکسیمم و به مقدار 
است، چنانکه در بند 1.14 دیدیم. در این فرکانس معادله 1.30 به صورت ساده زیر در می آید
که در آن 
دامنه سرعت رزونانس است. در فرکانس رزونانس معادله 1.28 به شکل زیر در می آید:
یادآوری می کنیم که در این فرکانس دامنه مسافت x ماکسیمم نیست و ماکسیمم آن به ازای مقدار دیگری از 
است که جمله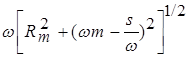 
را مینیمم می کند. می توان نشان داد که این فرکانس برابر است
در مواردی که مقاومت مکانیکی خیلی زیاد نباشد، 
در برابر 
قابل چشم پوشی است، و دامنه تغییر مکان را می توان در فرکانس رزونانس ، برابر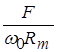 
من فرض کرد، که مقدار ماکسیمم است. هرگاه تغییرات توان متوسط را بر حسب فرکانس نیروی راننده با دامنه ثابت رسم کنیم منحنی نمایش آن نظیر منحنی نمایش توان الکتریکی بر حسب فرکانس در مدار الکتریکی RLC بدست می آید، که مقدار ماکسیمم آن برابر 
هم در فرکانس رزونانس است و در فرکانس های کمتر یا بیشتر از آن کاسته می شود.
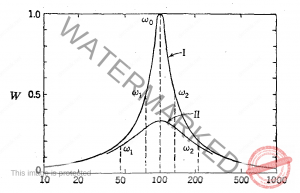
شکل 1.8 . منحنی رزونانس يك سيستم مکانیکی ساده. منحنی I مربوط به 3 = Q و کم منحني II مربوط به 1=Q و زیاد.
تیزی قله منحنی توان برحسب فرکانس نشانه ای از مقاومت مکانیکی به دست می دهد. اگر كوچك باشد، منحنی از حدود قله به سرعت نزول می کند و گویند دستگاه مکانیکی دارای رزونانس تیز است. اگر مقاومت مکانیکی زیاد باشد منحنی از اطراف خود به آهستگی نزول می کند، و گویند دستگاه دارای رزونانس پهن است. تیزی رزونانس را با عاملی به نام فاکتور کیفیت ، Q ، دقیق تر می توان تعریف کرد:
که در آن فرکانس رزونانس است، 
و 
دوفرکانس هستند که در بالا و پایین فرکانس رزونانس قرار دارند، و توان متوسط به ازای آنها به نصف مقدار توان روزنافس تقلیل می یابد. Q را می توان بر حسب پایاهای مکانیکی دستگاه تعیین کرد. از معادله 
روشن است که مقدار توان متوسط در ازای 
به نصف مقدار خود می رسد، و از آن نتیجه می شود
چون 
دو مقدار و از رابطه های زیر به دست می آیند.
اگر s را بین آن دو حذف کنیم این رابطه برقرار می شود :
و بنابراین،
که معادل است با 
، فاكتورکیفیت قرقرة القا. می توان نشان داد 
نسبت انرژی ماکسیمم نوسانگر در فرکانس رزونانس به انرژی مصرف شده در هر پریود است. اثبات این مطلب به عهده خواننده گذاشته شده است .
