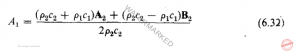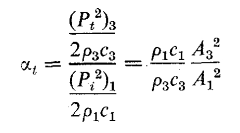مبانی آکوستیک
تراگسیل موج
بخش سوم ترا گسیل از سه محيط؛ تابش عمودی. این فرض می کنیم موج تا بش در جهت مثبت لا به سطح تخت 
، سطح جدایی محیط اول و دوم، به مختصات X=0 برخورد کند و از آن گذشته به محیط دوم برسد و همچنين به سطح تخت PP’ به مختصات X=1، سطح جدایی محیط دوم و سوم برخورد کند، و سپس از آن گذشته داخل محيط سوم شود (شکل 6.2). امپدانسهای مشخص محیطها را به ترتیب 
، 
و 
فرض می کنیم.
موج تابش در محیط اول را می توان با این معادله نمایش داد:
هنگامی که این موج به سطح جدایی دو محيط می رسد مقداری از انرژی آن بازتاب می کند و مقداری دیگر وارد محیط دوم می شود و این یکی به نوبه خود پس از برخورد به سطح 
، سطح جدایی محیطهای دوم و سوم به دو قسمت می شود؛ قسمتی بازتاب می یابد و قسمت دیگر به محیط دوم وارد شده به انتشار خود ادامه می دهد. اگر این پدیده را دقیقتر بررسی کنیم به این نتیجه می رسیم که مقداری از موج وارد شده در محیط دوم پس از عبور از آن از سطح X=1 بازتاب می یابد و به سطح 0=x بر می گردد و در برخورد به آن سطح مقداری از آن دوباره بازتاب یافته به محیط دوم باز می گردد و با موجی که قبلا از محیط اول در آن وارد شده است جمع می شود، و بقیه به محیط اول وارد شده با موج باز تاب موجود در آن جمع می گردد. این فراروند پی در پی ادامه می یابد تا جایی که پس از تعدادی كافي باز تاب و تراگسيل، حالت تعادلی از لحاظ انرژی موجی در محیط دوم پدیدار شود. از این پس و در این حالت است که می توان پذیرفت که مجموع انرژی موج باز تاب در محیط اول به اضافه موج ترا گسیل در محیط سوم برابر موج تا بش است. در این شرایط، موج باز تاب در محیط اول را می توان با معادله زیر نمایش داد
و موج ترا گسیل و بازتاب در محیط دوم با معادله های
و موج ترا گسیل در محیط سوم با معادله
مشخص می شود. یادآوری می کنیم که دامنه و فاز موجهای موجود در محیط اول و دوم در حالت تعادل با دامنه و فاز موجهای اولیه باز قاب در سطح X=0 تفاوت دارد. شرط مرزی پیوستگی فشار در سطح X=0 بدین رابطه منجر می شود
و شرط مرزی پیوستگی سرعت لحظه ای در این مرز به معادله زیر میرسد
همچنین، شرط پیوستگی فشار در سطح X=1 بدین نتیجه می رسد
و شرط پیوستگی سرعت لحظه ای در این مرز چنین خواهد شد
برای تعیین مقدار مختلط 
دامنه موج ترا گسیل در محیط سوم بر حسب 
لازم است مقدارهای 
و 
و 
را از چهار معادله بالا حذف کنیم. اگر دومعادله 6.28 و 6.29 را ترکیب کنیم حذف می شود و این معادله به دست می آید
همچنين از ترکیب دو معادله 6.30 و 6.31 این معادله ها به دست می آیند
اگر معادله های بالا را در معادله ی 6.32 بگذاریم، رابطه زیر به دست می آید
که چنین خلاصه می شود
مقدار کسر مختلط 
، معرف نسبت دامنه فشار موج تا بش به دامنه فشار موج ترا گسیل در محیط سوم است، و زاویه فاز آن اختلاف فاز بین موج در X=0 و موج ترا گسیل در X=1 را نشان میدهد. ضریب توان ترا گسیل 
بین محیط اول و محيط سوم بدین مقدار است
مقدار 
را می توان با جمع کردن مربعات مقادیر حقیقی و انگاری معادله ی 6.35 به دست آورد و در معادله بالا قرار داد که بدین نتیجه می رسد
معادله بالا در مورد خاص به اشکال مختلف مورد استفاده قرار می گیرد. یکی از آن موارد این است که محیط نهائی با محیط اول یکسان باشد؛ در این صورت
و در موردی که 
باشد می توان از 
در برابر جمله دیگر پرانتز چشم پوشیده
مثلا در موردی که بخواهند میزان ترا گسیل موج صوتی را از هوای اتاقی به هوای اتاق مجاور تعيين كنند از معادله فوق استفاده می کنند، و همچنین میزان ترا گسیل موجهای صوتی درون آب، پس از عبور از دیواری فولادی به آب موجود در طرف دیگر دیواره را به سيله این فرمول به دست می آورند مواد جامدی که فعلا در ساختمان دیوارهای اتاق به کار می روند نسبت به هوا دارای امپدانس مشخص زیادتری هستند، چنانکه پیوسته رابطة 
در فرانسهای معمولی صوتی و ضخامتهای معمولی دیوارها برقرار است. بنابراین در موردی که شاره هوا باشد معادله 6.37a باز هم خلاصه تر می شود
بالاخره در تمام مواردی که فرکانسها خیلی بالا و دیوارها زیاد قطور باشند 
است و به جای 
می توان 
به کار برد؛ و معادله بالا به صورت خلاصه تر، بدين عبارت منجر می شود
مثلا در فرکانسی 1000 مقدار را برای دیواری از بتون سیمانی به قطر 
برابر 0.2 است.
سرعت صوت در بتون سیمانی برابر 
است) . ممکن است با تصور ازدیاد امپدانس مشخص محیط اول،، به میزان راكتانس آکوستیکی 
اموز در سطح 0 = x و حذف محیط دوم به معادلهای مشابه معادله 6.37c رسید، و با معادلاتی که در 6.3 تشريح گردید مقادير و 
را به دست آورد. بنابراین، وجود مانعی مانند دیوار در مسیر عمودی موج به منزله اضافه کردن اندوكتانس در خط ترا گسیل موج است. در معادله 6.37c، حاصل 
را می توان چنگالی سطحی دیوار برحسب
دانست که با حرف 
معرفی می شود. همچنین به جای 
می توان بر حسب فرکانس f ، 
قرار داد. در این صورت این معادله به صورت زیر در می آید
که به کار بردن آن در عمل آسانتر و عملیتر است.
خواص ترا گسیل دیوار را در برابر موجهای صوتی معمولا با نشانه TL معرف ضريب کاهش ترا گسیل انرژی، نمایش می دهند که با این معادله تعریف می شود
که در آن 
شدت موج تابش و
شدت موج ترا گسیل است. ولی چون 
است، با استفاده از مقدار TL چنین می شود
اگر به جای 2 امپدانس مشخص هوا، 415، قرار دهیم و واحدها را چنان تبدیل کنیم که بر حسب پوند بر فوت مربع داده شود معادله ای که در عمل به سهولت مورد استفاده مهندسان قرار می گیرد به دست می آید
که با نتایج تجربی به دست آمده برای تابش عمودی موجهای صوتی بر دیوار توافق خوبی دارد. یاد آوری می کنیم که هر گاه فرکانس f مقدار جرم دیوار در واحد سطح دو برابر
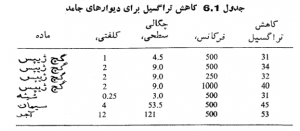
شود، TL به میزان 6db اضافه می شود. در اوضاع معمولی موجهای صوتی در اتاق منحصر عمود بر دیوارها منتشر نمی شود، بلکه امکان انتشار آن در تمام جهات اتفاقی، بیشتر است. در نتیجه ضریب کاهش تراگسیل از مقدار پیشبینی شده توسط معادله ی 6.40a کمتر است. جدول 6.1 مقدارهای ضریب کاهش ترا گسیل اندازه گیری شده در مورد دیوارهایی از جنسهای مختلف را نشان میدهد. معادله تجربی زیر برای محاسبه مقدار کاهش ترا گسیل در موردی که تابش در جهات اتفاقی به دیوار برسد به کار می رود
در تراگسيل موج در آب هر دو جمله مخرج معادله 6.37a قابل ملاحظه است و نمی توان از آنها چشمپوشید؛ مگر در مواردی که دیوار فاصل به میزانی نازك با فرکانسها چنان کم باشند که شرط
برقرار باشد. در این صورت معادله ی 6.37a خلاصه می شود و به صورت 
در می آید و معنی آن این است که موج تا بش در آب در عبور از دیواره انرژی خود را تقریبا ثابت نگه می دارد. از این خاصیت برای جادادن تراگذارهای صوتی در آب، در گنبدهایی معلق استفاده می کنند. جدار گنبد از فولاد پرداخته غیرقابل زنگی زدن در آب يا از لاستيك است. نازکی آن به میزانی است که کاهش انرژی صوتی در عبور از آن در آب دریا اندك باشد. شکل دیگری از معادله 6.36 در موردی به دست می آید که محیط میانی، امپدانس ویژه اش بیش از امپدانسهای ویژه محیط اول و محیط سوم باشد. همچنین ضخامت آن و امپدانس ویژه اش چنان باید باشد که شرایط 
و 
برقرار گردد. در این صورت معادله 6.36 بدین عبارت خلاصه می شود
این معادله معادل معادله 6.11 و معرف ضریب توان تراگسيل موجتي است که مستقیما از محيط یکم به محيط سوم وارد می شود، و می رساند که با انتخاب مناسب ضخامت و امپدانس ویژه تیغه ای از جامد، می توان دو شاره گازی یا آبگونی را برای جلوگیری از اختلاطشان جدا نمود بدون اینکه تداخل موجهای ترا گسیل در آن دو صورت گیرد. همچنین اگر محیط میانی به ضخامتی باشد که شرط 
( n عدد صحیح است) برقرار گردد برای همان رابطه به دست می آید، و این می رساند که ظاهرا ضخامتهایی با شرط فوق در محیط دوم در تراگسیل موج در فضای اول به فضای سوم بی تأثیر است، ولی با اینحال این خاصیت موقعی نمودار می شود که فرکانسهای موج، حوالی فرکانس 
متمرکز باشد. در صورتی که در مورد تیغه نازك برای تمام فرکانسهای پایینتر از حدی که با شرط مشخص شده باشد، بستگی به ضخامت تیغه ندارد. بالاخره هنگامی شرط 
(n .عدد صحیح است) برقرار باشد
و
و معادله 6.36 بدین عبارت خلاصه می شود:
این نسبت هنگامی برابر واحد می شود که این رابطه برقرار باشد
با شرط بالا توان ترا گسیل آکوستیکی به صد در صد می رسد. یعنی می توان انرژی آکوستیکی را از يك محيط به محیط دیگر با امپدانس مشخص مختلف بدون اتلاف انرژی منتشر کرده و در این حال باید امپدانس مشخص محیط میانی واسطه هندسی امپدانسهای مشخص محیطهای طرفین باشد. ولی این خاصیت موقعی برقرار است که فرکانسهای موج در حدود 
متمرکز باشند؛ یعنی ضخامت 
محيط ميانسی به مقدار
باشد. این روش برای به دست آوردن صد در صد موج تسرا گسیل در آکوستيك به وسيله محيط میانی به ضخامت ربع طول موج، شبیه روشی است که در اتپيك برای ساختن عدسیهای شیشه ای بدون بازتاب با پوشاندن آنها توسط لایه ای از مواد مناسب، مثلا فلورورهای قلیایی به ضخامت ربع طول موج، به کار می برند. زاویه فاز 
موجود در مقدار مختلط معرفی اختلاف فاز بين موجهای تابش و تراگسیل است که از رابطه زیر به دست می آید
نخست چنين به نظر می رسد که اختلاف فاز بين موج تا بشی و موج تراگسیل باید برابر باشد که معرف زمانی است که موج ضخامت محیط دوم را می پیماید. ولی چنانکه از معادله بالا هویداست چنین نیست. چه در حال تعادل معمولا در مرز 0=x تغییری در فاز بين موج تابش و موج ترا گسیل رخ می دهد.
