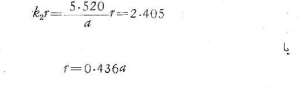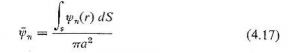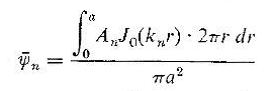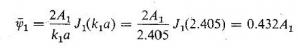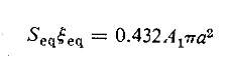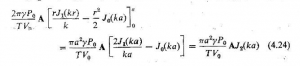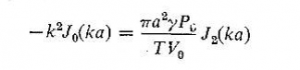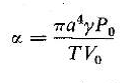مبانی آکوستیک
ارتعاش پوسته های گرد و ورقه ها
بخش سوم شرایط مرزی. شرط مرزی در لبه يك پوسته گرد طوری است که در 
و 
شود؛ بنابراین 
و از آنجا
پس فرکانس اصلی آن چنین خواهد شد
نسبتهای فرکانسهای فرعی به فرکانس اصلی بدین مقادیر است
و غيره چنانکه ملاحظه می شود، مانند ارتعاشهای عرضي يك ميله فرکانسهای فرعی، هارمونیکهای فرکانس اصلی نیستند. مقدار حقیقی تابع 
تغییر مکان پوسته را در مد اصلی ارتعاش خود، معرفی می کند
که در آن 
تغییر مکان دامنه در مرکز پوسته و 
به جای قرار 
گرفته است. حل کامل معادله موج شامل تمام مدهای ارتعاشی بدین صورت است
برای تمام مدهای ارتعاشی غیر از مد اصلی، دایره های گرهی داخلی در فاصله هایی به شعاع r می باشند بطوریکه این مقادیر ، 
را برابر صفر گرداند. مثلا برای اولین نت فرعی، تايع 
برای مقداری ا
باشد، صفر خواهد شد. و دایره گرهی آن به همين شعاع است. چنانکه از منحنی 
در شکل 4.3 هویداست، تغییر مکان منطقه بین دو گره با تغيير مكان منطقه بين دوگره مجاور در فاز مخالف هستند. هنگامیکه حلقه های داخلی بالا می روند حلقه های خارجی پایین می روند و بعكس. منتجه اینگونه ارتعاش آن است که هوای مجاور پوسته در فرکانسهای فرعی دارای تغيير مكان نتیجه جزئی است و بدینجهت پوست طبل در این فرکانسها بازده صدایی کافی ندارد؛ یعنی اینگونه صداها را کم منتشر می سازد. مقدار متوسط تغییر مکان سطح پوسته در هر مد ارتعاشی عاملی برای سنجش میزان قدرت انتشار پوسته در آن مد به دست می دهد و می توان آن را با عبارت زیر معرفی کرد
چون نقاط پوسته واقع در هر حلقه نوار واقع بین شعاع r و 
به يك دامنه 
هستند، مقدار متوسط تغییر مکان پوسته را با انتگرال زیر می توان محاسبه کرد
که مقدار آن با استفاده از جدول 4.1 چنين است
به عنوان مثال، مقدار 
دامنه متوسط را برای مد ارتعاش اصلی حساب می کنیم
یعنی چنانچه پیستون سختی به شعاع a با دامنه 
با فرکانس اصلی بالا به ارتعاش در آید، مقدار حجمی از هوا را که در اثر ارتعاش جابجا می کند برابر مقدار حجمی است که پوسته با فرکانس اصلی خود جا بجا می کند. همچنین می توان نشان داد که 
است. علامت منفی می رساند که متوسط دامنه برای مد ارتعاش دوم بر خلاف متوسط دامنه ارتعاشی من اصلی است. مقایسه و 
می رساند که اگر دو مد ارتعاشی اول و دوم در مرکز به يك دامنه باشند، یعنی ، قدرت انتشار در مدل اصلی بیش از مد بعدی است. در بسیاری مسائل مربوط به مطالعه منابع موجهای صوتی خصوصیات موج صوتی بیشتر بستگی به میزان حجم هوای جابجا شده دارد، و شکل حقیقی سطح مورد انتشار صوت زیاد مؤثر نیست. بدین جهت، هر منبع صوت را می توان به پیستون سادة معادلی بدل کرد که حاصل ضرب سطح آن 
و در دامنه معادل 
حجم هوای جابجا شده به وسیله سطح منبع را تعیین می کند و آن را دامنه تغییر مکان حجمی منبع می خوانند. در محاسبه بالا دامنه تغيير مكان حجمی مد اصلی پوسته بدین مقدار است
در بحث مربوط به ارتعاش پوسته که به معادله 4.16 منجر گری دید، فرض بر این بود که ثابت دامنه، 
، مقداری ثابت است، در پوسته های حقیقی چنین فرضی مورد ندارد چه، تأثیر نیروهای اصطكاك داخلی و همچنین نیروهای خارجی مربوط به پخش انرژی به صورت موجهای صوتی باعث میرا شدن مدهای ارتعاشی می گردد و دامنه هر يك به صورت اکسپنانسيل 
نزول می کند که می توان با همان روشی که در نوسانگر ساده در بند 1.13 بیان شده، به دست آورد. بطور کلی ثابت میرایی 
، یا ازدیاد فرکانس افزایش می یابد؛ چنانکه هر چه فرکانس بالا می رود میرایی سریعتر است. نقاره. نیروی مقاوم میراکننده که شرح آن گذشت یکی از انواع نیروهایی است که در ارتعاش پوسته مؤثر است. نوع دیگری از نیروهای مؤثر در ارتعاش، نیروی حاصل از تغییر فشاری است که در هوای موجود در فضای بسته محدود به پوسته، در اثر ارتعاش ايجاد می شود؛ مثلا در کاسه تار يا در میکروفون خازنی. به عنوان مثال ارتعاش پوست نقاره را مطالعه می کنیم. نقاره ظرف نیمکرهای است که دهانه آن از پوست کشیده شده ای پوشیده شده است. هنگامی که پوست به ارتعاش در می آید، حجم هوای درون ظرف کم و زیاد می شود و هوای درون آن را متراکم و منبسط می سازد. اگر سرعت شعاعی انتشار موجهای عرضی در سطح پوسته کمتر از سرعت انتشار صوت در هوا باشد، فشار حاصل از تراکم و انبساط هوای ظرف وارد به نقاط پوسته، یکنواخت است؛ یعنی تابعی از اوضاع شعاعی آن نقاط نیست، و مقدار آن فقط به تغییر مکان متوسط
بستگی دارد. هنگامی که سطح پوسته نقاره به شعاع r به مقدار متوسط تغییر مکان یابد، تغییر حجم هوای ظرف آن برابر 
می شود. اگر حجم ظرف نقاره را در حال تعادل برابر 
و فشار آن 
و تغییرات حجم را بی دررو فرض کنیم، فشار و حجم جدید هوای ظرف P وV، با رابطه زیر به و وابستگی دارند
که در آن 
نسبت گرمای ویژه هوای درون ظرف نقاره در فشار ثابت، به گرمای ویژه آن در حجم ثابت است. اگر از رابطه بالا نمو فشار را بر حسب نمو حجم به دست آوریم خواهیم داشت
اگر در معادله ی 
نیروی فشار بالا را وارد سازیم، بدین صورت خلاصه می شود
که در آن نشانه 
بجای اوپراتور لاپلاس در مختصات قطبی 
برای تابعی دارای قرینه دایره ای به کار رفته است. در این معادله و تابع مجموع مدهای ارتعاشی آزاد پوسته است که با معادله 4.16 معرفي شده و حل معادله 4.21 را مشکل ساخته است. هرگاه یکی از مدهای ارتعاشی را به تنهایی در نظر بگیریم حل آن ساده می شود. فرض کنیم که تنها ارتعاش با فرکانس 
موجود باشد، در این صورت حل معادله بالا را به این صورت می توان نوشت
که در آن 
فقط تابع r است. اگر آن را در معادله 4.21 قرار دهیم، بل با معادله زیر تعيين می شود
برای حل معادله بالا فرض می کنیم و به صورت زیر باشد
این فرض بدان جهت است که اگر سمت راست معادله ی 4.22 صفر باشد، حل آن به صورت 
است؛ و به علت وجود انتگرال در سمت راست معادله بالا، تابعی از a مثلا به صورت 
اضافه می کنند تا حل فوق با شرایط مرزی بهتر وفق دهد. با این فرض می توان به 
بدون در نظر گرفتن مقادیر مخصوصی از k تابع را برابر صفر کرد؛ و با این فرض سمت راست معادله 4.22 به صورت زیر خلاصه می شود
که در آن 
تابع بسل درجه دوم از نوع اول است. اگر را از معادله 4.23 در معادله ی 4.22 قرار دهیم، چنين خلاصه می شود
یاا
که در آن
a ثابتی است بدون بعد و بستگی به چگونگی نیروهای برگرداننده حاصل از تراکم هوای ظرف و کشش پوسته نقاره دارد. هر گاه حجم ظرف نقاره یا کشش پوسته آن زیاد باشد، مقدار a كوچك است . در حد، هنگامی که a به صفر نزديك باشد فرکانسهای مربوط به 
همان فرکانسهای آزاد پوسته هستند؛ چنانکه شرح آن گذشت.
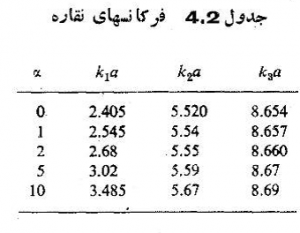
جدول 4.2 مقادیر ka راکه در معادله 4.25 صادق هستند، به ازای مقادیر a به از 0 تا 10 نشان میدهد. چنانکه ملاحظه می شود، وجود کاسه نقاره مقادیر عددی ka و بنا بر این مقادیر عددی فركانسها را افزایش میدهد. و این امر نیز پیش بینی پذیر است؛ چه، جمله اضافی در معادله 4.21 با تغيير مكان متناسب است و به منزله نوعی سختی در نوسانگر محسوب می شود. بعلاوه تأثیر آن در فرکانس اصلی بیش از سایر فرکانسهاست. این امر نیز مسلم است، زیرا هر چه مد ارتعاشی پوسته بالاتر رود، و در نتیجه تعداد بیشتری از قطعات با فاز مخالف ارتعاش یا دند. دامنه متوسط کمتر می شود.
