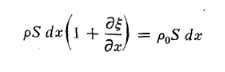مبانی آکوستیک موج های آکوستیکی تخت بخش اول موجهایی که احساس صوت ایجاد می کنند از جمله انواع گوناگون موج هایی به شمار می روند که در اثر آشفتگی فشار در هر شاره تراکم پذیر ایجاد می شوند، و در آن انتشار می یابند. بعلاوه موج های فراصوتی، که فرکانس آنها بیش از فرکانسهای صوتی است و به گوش شنیده نمی شوند، همچنین موجهای شدیدی که در نزدیکی جتها و موشکها پدیدار می شوند و تأثیرشان در گوش بیشتر احساس درد ایجاد می کند تا احساس صوت، و موجهای ضربه ای که به وسیله انفجارها یا هواپیماهای بسیار تند پرواز پدید می آیند نیز وجود دارند. موجهای آکوستیکی در شارهها از بسیاری جهات از موجهایی که در فصلهای پیش مورد بحث قرار گرفتند متمایز ند. یکی اینکه این موجها سه بعدی هستند، و از این لحاظ رفتار آنها نسبت به موجهای یك بعدی، مانند موجهای تارهای مرتعش و میله، و موجهای دو بعدی، مانند موجهای منتشر، در پوسته و ورقه، پیچیده تر است. دیگر آنکه این موجها طولی هستند، یعنی نوسان مولكولها و امتداد رفت و برگشت آنها بر امتداد انتشار موج منطبق است، و مانند موجهای طولی میله سبب تراكم و انبساط متناوب مناطق شاره می گردند. در حالی که در موجهای عرضى امتداد بالا و پایین رفتن ذرات عمود بر انتشار موج است. بعلاوه در شاره تغییر فشار با روشهای گوناگونی که بستگی بامکان تغییر شکلهای فیزیکی آن دارد دست می دهد. در حالی که در جامد این روش ها محدودتر است. بالاخره در شاره نیروی برگرداننده ای که سبب انتشار موج می گردد نیرویی است حاصل از مقاومت همه جانبه که در اثر تراکم آن ایجاد می گردد. این عوامل باعث می شوند که موج حاصل در يك شاره از بسیاری جهات از پدیده های موجی که در پیش شرح آنها گذشت متمایر باشد و حدود پیچیدگی آن وسیعتر گردد. بهتر است بحث خود را از موج تخت که ساده ترین آنهاست آغاز کنیم. خاصیت مشخص این موج آن است که فشارهای آکوستیکی، تغییر مکان ذرهها، تغییر چگالی، و غیره، در همه نقاط واقع در هر سطح عمود بسر امتداد ارتعاش به يك فاز و به يك دامنه هستند. موج تخت را می توان به وسیله پیستونی که شاره درون لوله ای را به ارتعاش در می آورد ایجاد کرد. هر نوع سطح موج واگرا در محیط يكنواخت را می توان موج تخت دانست؛ در صورتی که با منبع خود دارای فاصله نسبتا زیادی باشد. رفتار الإستيك شاره ها. چنانکه اشاره شد، موجهای آکوستیکی تخت بسیاری خواص مشترك با موجهای طولی منتشر در میله ناز دارند. بدین جهت، ممکن است معادله انتشار موج تخت حاصل درون شاری موجود در لوله ای به مقطع ثابت را با همان روشی که در مورد انتشار موج در میله (بند 3.3 )، برای یافتن معادله انتشار موج به کار بردیم، به دست آورد. بنابراین لازم است قبلاً رابطه ای بین تغيير فشار درونی شاره و تغییر شکل شاره بيا بيم؛ چنانکه در میله نیز معادله 3.5 نماینده تغییر شکل طولی میله است. این معادله را می توان با ترکیبی از معادله های معرفی خواص ترمودینامیکی شاری با در نظر گرفتن اصل بقای جرم به دست آورد. در یافتن و حل معادله های مربوط به انتشار موجهای تخت در امتدادx ، نشانه های اختصاری زیر را به کار می بریم. x د مختصات ذره ی مرتعش در وضع تعادل خود ![]() تغییر مکان دره نسبت به وضع تعادل در امتداد محور x ها
تغییر مکان دره نسبت به وضع تعادل در امتداد محور x ها ![]() سرعت لحظه ای در مرتعش که برابر است با
سرعت لحظه ای در مرتعش که برابر است با ![]() 1/4
1/4 ![]() مجرم ویژه لحظه ای شاره در هر نقطه
مجرم ویژه لحظه ای شاره در هر نقطه ![]() جرم ویژه ثابت شاره در حال تعادل S تراکم در هر نقطه از شاره، که با رابطۀ زیر معرفی می شود
جرم ویژه ثابت شاره در حال تعادل S تراکم در هر نقطه از شاره، که با رابطۀ زیر معرفی می شود
P فشار لحظه ای در هر نقطه ![]() فشار ثابت شاره در حال تعادل P تغییر فشار شاره نسبت به فشار تعادل،
فشار ثابت شاره در حال تعادل P تغییر فشار شاره نسبت به فشار تعادل، ![]() ، که فشار آکوستیکی نامیده می شود
، که فشار آکوستیکی نامیده می شود
سرعت انتشار موج مقصود از ذره در اینجا حجم کمي از شاره است، و چنان کوچک است که می توان تغييرات آکوستیکی مانند فشار، چگالی، و سرعت را برای تمام مولکولهای آن در هر لحظه برابر گرفت. چنين ذرهای خود دارای میلیونها مولکول است و به میزانی بزرگی است که بتوان آن را شاری پیوسته ای تصور کرد. در آنچه خواهد آمد، از تأثیرات نیروهای گرانشی چشمپوشی می شود، و بنا بر این مقادیر ![]() و
و ![]() در تمام نقاط شاره يکسان گرفته می شوند. همچنین شاره را همگن، ایزوتروپ۲، و کاملا الاستيك، یعنی بدون نیروهای مصرف کننده ، مانند نیروهای حاصل از چسبندگی وهدایت گرما فرض می کنیم. وانگهی، بحث را به موردهایی محدود می سازیم که دامنه موجها كوچك باشد، و تغییرات چگالی نسبت به مقدار آن در حال تعادل، جزئی گرفته شود. هنگامی که سطح موج در امتداد محور x حرکت می کند، سطوحی از مولکولهای شارة مجاور و موازی سطح موج از حالتهای تعادل خود تغییر مکان می دهند و عموما این تغییر مكانها برای نقاط واقع بر هر سطح برابر هم و تابعی از دو متغیر x ، معرف وضعیت، و t معرف زمان هستند، که می توان آن را با تابع
در تمام نقاط شاره يکسان گرفته می شوند. همچنین شاره را همگن، ایزوتروپ۲، و کاملا الاستيك، یعنی بدون نیروهای مصرف کننده ، مانند نیروهای حاصل از چسبندگی وهدایت گرما فرض می کنیم. وانگهی، بحث را به موردهایی محدود می سازیم که دامنه موجها كوچك باشد، و تغییرات چگالی نسبت به مقدار آن در حال تعادل، جزئی گرفته شود. هنگامی که سطح موج در امتداد محور x حرکت می کند، سطوحی از مولکولهای شارة مجاور و موازی سطح موج از حالتهای تعادل خود تغییر مکان می دهند و عموما این تغییر مكانها برای نقاط واقع بر هر سطح برابر هم و تابعی از دو متغیر x ، معرف وضعیت، و t معرف زمان هستند، که می توان آن را با تابع ![]() نمایش داده نخست رابطه ای بین این تغيير مكانها و تغییرات چگالی شاره به دست می آوریم. بدین منظور لایه ای از شاره به مقطع قائم S واقع بین دو سطح موازی به اوضاع x و
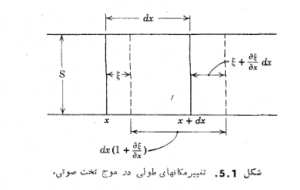
نمایش داده نخست رابطه ای بین این تغيير مكانها و تغییرات چگالی شاره به دست می آوریم. بدین منظور لایه ای از شاره به مقطع قائم S واقع بین دو سطح موازی به اوضاع x و ![]() در حال تعادل در نظر می گیریم (شکل 5.1). جرم این لایه برابر
در حال تعادل در نظر می گیریم (شکل 5.1). جرم این لایه برابر ![]() است. اکنون فرض می کنیم هنگامی که موج آکوستیکی در حرکت است صفحه ای را که در
است. اکنون فرض می کنیم هنگامی که موج آکوستیکی در حرکت است صفحه ای را که در ![]() مستقر است به اندازه
مستقر است به اندازه ![]() تغییر مکان می دهد ( به طرف راست). پس حجم لایه جدید برابر
تغییر مکان می دهد ( به طرف راست). پس حجم لایه جدید برابر ![]() خواهد بود. تغيير حجم سبب تغییر چگالی می گردد ولی جرم لایه در این تغییر ثابت می ماند. چون چگالی فعلى شاره را 2 فرض کنیم می توان نوشت
خواهد بود. تغيير حجم سبب تغییر چگالی می گردد ولی جرم لایه در این تغییر ثابت می ماند. چون چگالی فعلى شاره را 2 فرض کنیم می توان نوشت
چون به جای ![]() از معادله 5.1 حاصلضرب
از معادله 5.1 حاصلضرب ![]() را قرار دهیم و مقدار مشترك
را قرار دهیم و مقدار مشترك ![]() را از دو طرف حذف کنیم، معادله زیر به دست خواهد آمد
را از دو طرف حذف کنیم، معادله زیر به دست خواهد آمد
مقدارهای S و ![]() بسیار کوچکند، و حتی برای صوتهای بسیار شدید در مرز بالای شنوایی که سبب ایجاد درد در گوش انسان می گردد، مقدار آنها از
بسیار کوچکند، و حتی برای صوتهای بسیار شدید در مرز بالای شنوایی که سبب ایجاد درد در گوش انسان می گردد، مقدار آنها از ![]() تجاوز نمی کند. بنابراین می توان در معادله بالا از حاصلضرب آن دو چشم پوشید، و معادله را بدینصورت کوتاه کرد
تجاوز نمی کند. بنابراین می توان در معادله بالا از حاصلضرب آن دو چشم پوشید، و معادله را بدینصورت کوتاه کرد
.شکل 1-5 تغییر مکانهای طولی در موج تخت صوتی
این معادله شکل خاصی از معادله مهم هیدرودینامیک به نام معادل پیوستگی است و می رساند که اگر سطحی از مولکولهای شاره واقع در سمت راست نقطه معینی بیش از سطحی از مولکولهای واقع در سمت چپ آن نقطه به سوی راست تغییر مکان دهد، یعنی فاصله این دو سطح پس از تغییر بیش از فاصله آن دو در حال تعادل باشد، ![]() مثبت است، و چگالی شاره کم می شود. خاصیت دیگر شاره ها که هنگام یافتن معادله موج دخالت می کند خاصیت ترمودینامیکی آن است که رابطه بین تغییرات فشار و چگالی را مشخص می کند. بطور کلی، برحسب اینکه در چه شرایطی این رابطه را بررسی کنیم، ارتباط آن دو با یکدیگر متفاوت خواهد بود. مثلا برای گاز کامل در فراروند همدما رابطه
مثبت است، و چگالی شاره کم می شود. خاصیت دیگر شاره ها که هنگام یافتن معادله موج دخالت می کند خاصیت ترمودینامیکی آن است که رابطه بین تغییرات فشار و چگالی را مشخص می کند. بطور کلی، برحسب اینکه در چه شرایطی این رابطه را بررسی کنیم، ارتباط آن دو با یکدیگر متفاوت خواهد بود. مثلا برای گاز کامل در فراروند همدما رابطه ![]() در حالی که در فراروند بی در رو
در حالی که در فراروند بی در رو ![]() برقرار است . حال باید دید در انتشار موج در شاره انبساط و تراکم متناوب لایه ای مانند Sdx در شکل 5.1 با چه فرارو ندی صورت می گیرد. عموما هر تراکمی در حجم شاره مستلزم انجام کاری است که به گرما مبدل می گردد و اگر به ملایمت انجام نشود که وقت کافی برای تبادل آن با محیط خارج موجود باشد، سبب بالارفتن دما می گردد. هنگامی که موج آکوستیکی در شاره انتشار می یابد، گرادیان دما بين نقعلة مجاور منقبض شده و نقطة مجاور منبسط شده ، نسبتا کوچک است؛ در نتیجه تا زمانی که لايه منقبض شده هنوز منبسط نگشته، مقدادی انرژی گرمایی از آن به قسمت مجاور خود انتشار می یابد. در تحت چنین شرایطی می توان فراروند بالا را بی دررو دانست. به منظور عمومیت دادن نتایج، چنانکه در باره همه گونه شاره، مانند آبگونها، گازهای حقیقی مثل گازهای کامل صادق باشد روش بی دررو را با معادلة
برقرار است . حال باید دید در انتشار موج در شاره انبساط و تراکم متناوب لایه ای مانند Sdx در شکل 5.1 با چه فرارو ندی صورت می گیرد. عموما هر تراکمی در حجم شاره مستلزم انجام کاری است که به گرما مبدل می گردد و اگر به ملایمت انجام نشود که وقت کافی برای تبادل آن با محیط خارج موجود باشد، سبب بالارفتن دما می گردد. هنگامی که موج آکوستیکی در شاره انتشار می یابد، گرادیان دما بين نقعلة مجاور منقبض شده و نقطة مجاور منبسط شده ، نسبتا کوچک است؛ در نتیجه تا زمانی که لايه منقبض شده هنوز منبسط نگشته، مقدادی انرژی گرمایی از آن به قسمت مجاور خود انتشار می یابد. در تحت چنین شرایطی می توان فراروند بالا را بی دررو دانست. به منظور عمومیت دادن نتایج، چنانکه در باره همه گونه شاره، مانند آبگونها، گازهای حقیقی مثل گازهای کامل صادق باشد روش بی دررو را با معادلة ![]() معرفی می کنیم ،که دیفرانسیل آن بدینصورت است
معرفی می کنیم ،که دیفرانسیل آن بدینصورت است
که در آن ![]() ضریب زاویه منحنی تغییرات فشار بر حسب چگالی در نقطه
ضریب زاویه منحنی تغییرات فشار بر حسب چگالی در نقطه ![]() است. در تغییرات جزئی فشار موجهای آکوستیکی، می توان به جای dp فشار آکوستیکی p و به جای
است. در تغییرات جزئی فشار موجهای آکوستیکی، می توان به جای dp فشار آکوستیکی p و به جای ![]() از معادله 5.1 ،
از معادله 5.1 ،![]() قرار داد
قرار داد
![]() مساوی مربع ابعاد سرعت است و آن را با
مساوی مربع ابعاد سرعت است و آن را با ![]() نمایش میدهیم
نمایش میدهیم
بنابراین
که معادله سهمی است و فشار آکوستیکی و تراکم را به هم مربوط می سازد. چون به جای s مقدار آن ![]() از معادله
از معادله ![]() را قرار دهیم، فشار آکوستیکی بر حسب تغيير مكان به دست می آید
را قرار دهیم، فشار آکوستیکی بر حسب تغيير مكان به دست می آید
مقایسه معادله بالا با معادله 3.5 شباهت رابطه بین انبساط و فشار تراكم را در موج های تخت طولی در يك شاره و يك ميله روشن می سازد.