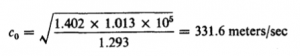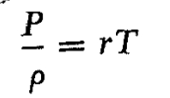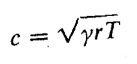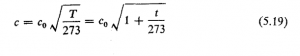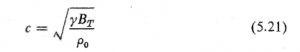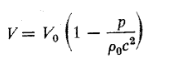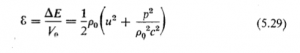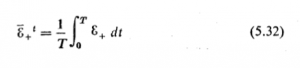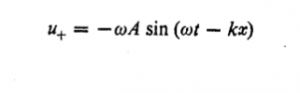مبانی آکوستیک
موج های آکوستیکی تخت
بخش سوم سرعت انتشار صوت در شاره ها، سرعت انتشار موج آکوستیکی را در يك شاره با ثابت c ) در 5.3 معرفی کردیم
که در آن 
برای فراروند بیدار و در شرایط تعادل فشار و چگالی محاسبه می شود. سرعت انتشار یکی از خواص مشخص شاره به شمار می رود، و به جنس آن از لحاظ الاستیسیته و همچنین متغیرهای ترمودینامیکی آن از قبیل دما، فشار، و چگالی بستگی دارد. سرعت انتشار موجهای آکوستیکی معمولی و قابل احساس به وسیله گوش انسان به فرکانس و دامنه فشار یا تغییر مکان بستگی ندارد. هنگامی که موج صوتی در گازی انتشار می یابد قانون گازهای کامل در فر اروند بیدررو صورت مخصوصی از معادله 5.5 به دست می دهد. قانون بالا را بدین صورت می توان نوشت
که در آن 
نسبت گرمای ویژه در فشار ثابت به گرمای ویژه در حجم ثابت است و K مقدار ثابتی است. از مشتق را به بالا به دست می آید
اگر عبارت را برای شرایط تعادل فشار و چگالی یعنی 
و
در معادله ی 5.5 بگذاریم، سرعت انتشار با رابطه زیر مشخص خواهد شد
در جدول ضمیمه ها مقدارهای و در °C 
و فشار متعارفی 
نیوتن بر متر مربع نموده شده است. پس، رابطه بالا سرعت انتشار صوت در هوا را بدین مقدار به دست می دهد
که با مقداری که از آزمایشهای مکرر به دست می آید با تقریب خوبی منطبق است؛ و این می رساند که فرض ابتدایی ما که گفتیم انبساط و تراکم، در انتشار موج، با فراروند بی دررو صورت می گیرد، صحیح است. در بسیاری از گازها نسبت 
به فشار بستگی ندارد. یعنی اگر فشار دو برابر شود چگالی نیز دو برابر می گردد و نسبت آن دو ثابت می ماند، و در نتیجه سرعت انتشار بستگی به فشار بارومتری ندارد. همچنین اگر هوا همگن و به يك دما باشد، سرعت انتشار صوت بستگی به ارتفاع نخواهد داشت. هيچيك از دو فرض بالا در عمل صادق نیست، یعنی ترکیب هوا در نقاط مختلف یکسان نیست و دمای آن نیز برحسب ارتفاع تغییر می کند. ولی تغییر حاصل در اثر تغییر دما از تغییر آن در اثر تغییر ترکیب، نمایانتر است که می توان به طریق زیر به دست آورد. یکی از اشکال قانون گازهای کامل بدینصورت است
که در آن r ثابت گاز مربوط به جنس آن و T دمای مطلق بر حسب درجه کلوین (K)، یعنی 
است، که در آن دما بر حسب سانتیگراد (°C) است. با در نظر گرفتن رابطه بالا سرعت چنین نوشته می شود
و این می رساند که سرعت انتشار صوت با جذر دمای مطلق آن متناسب است. رابطه C ، سرعت انتشار در T درجه کلوین، و 
سرعت انتشار در ℃0 چنین است
هرگاه دمای سانتیگراد نسبت به 273 كوچك باشد، معادله بالا را به صورت تقریبی زیر می توان نوشت
برای هوا 
برابر 
است و می توان نوشت
پیشبینی نظری سرعت صوت در آبگو نها دشوارتر از گازهاست. ولی معادله ای مشابه معادله 5.18 در مورد اینگونه شاره ها می توان به دست آورد که چنین است
که در آن 
,B مدول تراکم همدماست که برای اندازه گیری تراکم آبگو نها به کار می رود، و مقدارهای آن و همچنین مقدارهای کمیتهای دیگر در معادله بالا برای بعضی از آبگو نها در جدول I ضمیمه ها نموده شده است. این مقادیر بستگی به دما و فشار دارند. بنا براین سمعت صوت در آبگو نها با دما و فشار تغییر می کند. نظریه ساده ای برای پیشبینی این تغییرات به دست نیامده است. ولی معادله تجربی زیر سرعت صوت را در آب مقطر در فشار يك جو به دست می دهد
که در آن tف دما بر حسب سانتیگراد و c در حد متر بر ثانیه است، و آن را در فاصله °C 0 تا C° 60 با اشتباهی کمتر از 0.2 درصد سرعت صوت، می توان محاسبه کرد. چگالی انرژی موجهای تخت. انرژی موجود در شاره در اثر انتشار موجهای آکوستیکی شامل دو نوع انرژی جنبشی و انرژی پتانسیل است، که اولی در اثر حرکت ذرات شاره، و دومی در اثر تراکم آن پدیدار می شود. حجم کوچکی به مقدار 
ما مشابه آنچه در 5.2 به شکل لایه ای به قطر dx در نشر گرفتیم اختيار می کنیم، که در آن سرعت تمام ذره ها را می توان یکسان و به مقدار u گرفت. انرژی جنبشی حاصل از انتشار موج در آن چنین است
که در آن حجم ذره پیش از رسیدن موج به آن است و برابر 
می باشد. هنگامی که لایه بالا در اثر انتشار موج انبساط و تراکم می یابد، حجم آن V با معادله زیر تغییر می کند
چنانکه شرح آن در 5.2 گذشت، تغییر انرژی پتانسیل در اثر تغییر حجم بالا این اندازه است:
علامت منها می رساند که در اثر کار انجام یافته برای تراکم، حجم لایه کاهش می یابد، و انرژی پتانسیل با فشار آکوستیکی مثبت، افزایش پیدا می کند. برای حل انتگرال بالا لازم است دو متغير p و V را به يك متغير تبدیل کنیم. مثلا از معادله 5.6 به جای 
در معادلة 5.24 مقدار 
pf2c2 سه را قرار می دهیم
که دیفرانسیل آن چنین است
اگر مقدار dv را در معادله 5.25 قرار دهیم، انتگران آن قابل حل می گردد
انرژی آکوستیکی کل موجود در حجم 
چنین خواهد بود
و چگالی انرژی بر حسب ژول بر متر مکعب به مقدار زیر است :
برای تعیین چگالی لحظه ای انرژی هنگام انتشار موج در شاره در دو جهت مثبت و منفى x ، لازم است مقدارهای u و p را از معادله های 
و 
در معادله ی 5.29 قرار دهیم. ولی اگر دو موج را جدا از هم در نظر بگیریم، محاسبه بسیار ساده تر می شود. مثلا اگر موج تخت در جهت به انتشار یابد مقایسه بین معادله های و رابطه ی 
را بر حسب u به دست می دهد، که عبارت است از 
با قرار دادن آن در معادله 5.29، u چگالی انرژی در موج پیشرونده چنین به دست می آید
که در آن علامت + نشانه عبور موج در جهت مثبت محور x است. همچنین در مورد موج پسرونده، یعنی موجی که در جهت منفی محور x حرکت می کند، می توان نوشت: 
و از آنجا
بنابراین چگالی لحظه ای انرژی آکوستیکی در موردی که هر دو موج حاضر باشند، چنين است.
سرعت لحظه ای ذره در مورد موج تحت پیشرونده در جهت مثبت محور x، تابعی از وضع ذره و زمان است. بنابراین، چگالی انرژی 
، در همه نقطه ها و همه جهت ها ثابت نیست. مقدار متوسط زمانی آن در هر نقطه چنين است
که در آن انتگرال در زمان T که معرف يك دوره کامل از موج هارمونيك است محاسبه می شود. از معادله می توان نوشت
