مبانی آکوستیک
رزوناتورها
بخش سوم امپدانس آکوستیکی توزیع شده وقتی ابعاد اجزای يك دستگاه آکوستیکی در مقایسه با طول موج کوچک نباشد نمی توان برای دستگاه ثابتهای کلی در نظر گرفت، بلکه ثابتهای توزیع شده در آن خودنمایی می کنند. ساده ترین دستگاه از این نوع دستگاهی است که در آن موج های تخت در يك لوله طويل منتشر می شوند. اگر موجها در امتداد مثبت x منتشر شوند نسبت فشار آکوستیکی به سرعت ذره ای از امپدانس ویژه محیط، 
، به دست می آید؛ و بنا بر این امپدانس آکوستیکی در هر مقطع قائم S لوله این است. 
انتشار موج های تخت در چنین لوله ای شبیه انتشار جریانهای پرفرکانس در امتداد خط قراگسيل است. می توان محیط لوله را دارای اینرتانس توزیع شده 
در واحد طول دانست؛ چنانکه
باشد. همچنین محیط لوله دارای نرمش آکوستیکی توزیع شده 
در واحد طول است؛ چنانکه 
باشد. کاربرد معادله معروف امپدانس ویژه مباني آكوستيك خط تراگسيل در مسئله مشابه آکوستیکی، امپدانس موج های تخت را در لوله بدین مقدار به دست می دهد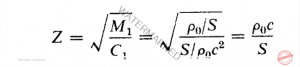 
که با معادله 8.21 موافقت دارد. بعلاوه چنانکه در بخشهای آینده نشان داده خواهد شد بازتاب و تراگسیل موج های صوتی در نقطه ای که در آن امپدانس آکوستیکی لوله تغییر می کند شبیه رفتار موج های جریان در نقطه ای از خط تراگسیل است که در آن تغییر ناگهانی در ابعاد رخ داده باشد، یا به امپدانسی سوای امپدانس ویژه خط رسیده باشد. بازتاب موجها در لوله. فرض کنیم در نقطه و در امتداد لوله امپدانس آکوستیکی از مقدار ویژه خود به 
تغییر یافته باشد که بنا بر نوع خاص تغییر حاصل در لوله ممکن است حقیقی یا مختلط باشد. هرگاه موج تا بش اصلی در امتداد مثبت محور x منتشر شده و با معادله زیر معرفی شود 
موج باز تایی در جهت منفی محود x با این معادله ایجاد خواهد شد 
سرعتهای حجمی شاره مربوط به این دو موج عبارتند از 
هنگامی که هر دو موج تابش و بازتاب در لوله موجود باشند تغییر فاز آنها از نقطه ای به نقطه ای دیگر سبب تغییر امپدانس از نقطه ای به نقطه دیگر می شود، برعکس حالتی که در آن فقط موج تابش حاضر باشد؛ چه در این صورت امپدانس آکوستیکی در تمام نقاط به يك اندازه است. عبارت کلی معرف امپدانس آکوستیکی هنگامی که هر دو موج موجود باشند این است 
در مقطع قائم لوله که در آن امپدانس تغییر می یابد شرایط معمولی پیوستگی فشار و سرعت حجمی را می توان با شرط پیوستگی نسبتهاشان، يعني باشرط پیوستگی امپدانس، معرفي کرد. بنابراین فازها و دامنه های موج های تابش و بازتاب باید چنان مربوط شوند که معادله 8.24a برابر شود. بدون کاهش در کلیت قضیه، مبدأ مختصات را می توان به نقطه ای که در آن امپدانس تغییر می یابد منتقل کرد. در این صورت معادله 8.24a برابر 
می شود که در آن 
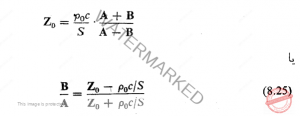ضریب توان بازتاب صوتی 
در نقطه ای که امپدانس آکوستیکی در آن تغییر می یابد بدین مقدار است 
که در آن جایگزین 
مجموع مقدار حقیقی ومقدار انگاری آن شده است. همچنین ضري توان بازتاب 
برابر 
این رابطه معرفی می شود 
گوشزد می کنیم که هريك ازسه معادله بالا از لحاظ شکل شبیه معادله هایی است که در بخش 6.3 به دست آمده ومعرف بازتاب موج های تختی است که با تابش عمودی از محیط اول به محیط دوم با امپدانس ویژه مختلف وارد می شوند. تنها اختلاف بين معادله های 8.25، 8.26، و 8.27 و معادله های نظیر آنها در بخش 6.3 این است که پارامترهای امپدانس آکوستیکی جایگزین پارامترهای امپدانس آکوستیکی ویژه شده اند. به عنوان مثال این معادله ها را در انتشار موج های تخت در لوله ای به مقطع قائم
به کار بریم که وارد لوله ای دیگر به مقطع قائم 
می شود، چنانکه در شکل 8.3 نمودار است. وقتی طول موج در مقایسه با قطر هر يك از لوله ها بزرگ باشد می توان فرض کرد امپدانس آکوستیکی موج های تابش در محل اتصال دو لوله برابر امپدانس آکوستیکی موج های تخت در لوله دوم 
باشد. لازمه این فرض این است که لوله دوم یا دارای طول بینهایت باشد یا چنان ختم شود که موج های بازتاب از آن ایجاد نشود، وسبب تولید موج های ایستاده نگردد. بعلاوه از تغییر شکل سطوح موج به صورت همگرا یا واگرا در سطح اتصال دو لوله چشم پوشی شود. چون مقدار را در معادله های کلی پیش قرار دهیم معادله های مربوط به این حالت خاص به دست می آیند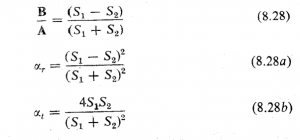 
باید در نظر داشت که معادله های بالا در موردی که ابعاد هريك از سطوح یا به طول موج نزديك باشد قابل قبول نیست، چه در این حالت امپدانس آکوستیکی در محل اتصال دولوله برابر 
نخواهد بود. بالاخره در موردی که طول موج بسیار کوچکتر از قطر لوله کوچک باشد ضریب تو اگسيل أز لوله بزرگتر به مقطع به لوله کوچکتر به مقطع درست برابر نسبت سطوح آنها، 
خواهد شد. این رابطه از این فرض نتیجه می شود که کسری از سطح موج تا بش در لوله اول در برخورد به دهانه تمام تراگسيل يافته ، در صورتی که باقیمانده آن در کنار سخت ارتباط دو لوله بازتاب یافته است. همچنین چنانچه تا پیش از لوله کوچک به طرف لوله بزرگ باشد در فرکانسهای بالا تر اکسیل به 100 درصد نزدیک می شود. . هر گاه لوله ای در نقطه به جدار سختی منتهی شود 
و 
می شود، و دامنه فشار موج باز تاب برابر دامنه فشار موج تابش می گردد، و در نقطه فشارهای موج های تابش و بازتاب پیوسته همفازند. از طرف دیگر جریانهای حجمی در این وضع پیوسته ° 180 با هم اختلاف فاز دارند، و جدار در وضع گره سرعت حجمی قرار دارد و این موضوع روشن است. اگر دهانه لوله باز باشد و به لبه بینهایتی ختم شده باشد، امپدانس انتهایی همانند امپدانس پیستونی است که در دیوار بیکران کارگذارده باشند، یعنی 
و در نتیجه 
در فرکانسهای بالا که 
است تابع مقاومت پیستون و تابع راكتانس 
است چنانکه 
می شود. توان بازتاب بسیار اندك است B/A و در نتیجه تقريبا تمام توان آکوستیکی از دهانه باز لوله پخش می شود. از طرف دیگر، در فرکانسهای کم که 
باشد، می توان به جای 
و به جای 
، 
به کار برد. در این حالت 
هنگامی که 
باشد 
می شود و این می رساند که دامنه فشار موج بازتاب اندکی کمتر از دامنه موج تابش است. در نقطه x=0 فشارهای آنها با هم اختلاف فازی نزديك به ° 180 دارند، و در نتیجه موج تراکمی به موج انبساطی بدل می شود. برعکس سرعتهای حجمی، تابش و بازتاب در دهانه لوله تقریبا همفاز ند؛ چنانکه در این وضعیت تقريبا شکم سرعت حجمی موجود است. چون دامنه سرعت حجمی در دهانه پیوسته دو برابر سرعت حجمی موج تا بش است مقاومت آکوستیکی به قدری کوچك می شود که ضریب توان تراگسیل که بدین عبارت به دست می آید 
نیز كوچك می گردد. چون از جمله های 
به بالا از میخرج در برابر واحد چشمپوشی کنیم عبارت بالا ساده تر می شود 
هنگامی که طول موج 
موج تا بیش در مقایسه با شعاع a لوله بزرگ باشد تنها درصد کوچکی از توان آکوستیکی از دهانه کناره دار لوله خارج می شود، و بقيه درون لوله بازتاب می یابد؛ و این نتیجه با نتایج بخشهای 7.5 و 7.14 مطابقت دارد، یعنی منابعی که ابعادشان نسبت به طول موج صوت كوچك باشد از لحاظ پخش انرژی صوتی ضعیفند. در فرکانسهای کم که باشد، آزمایش و حساب نشان میدهد که امپدانس آکوستیکی لوله بدون کناره تقريبا بدین مقدار است 
به آسانی می توان دریافت که ضریب ترا گسیل در انتهای چنین لوله ای این است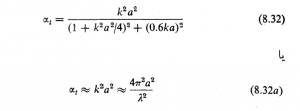 
و این می رساند که وجود کناره وسیعی در انتهای لوله، تابش صوت را در فرکانسهای کم تقریبا دو برابر می سازد. گوشزد می کنیم که در لوله ای که به زائدة بوقی شکلی متصل شود که قطر مقطع آن به تدریج زیاد شود توان تراگسيل فرکانس پایین در آن باز هم افزایش می یابد
