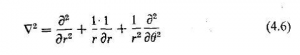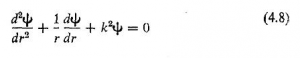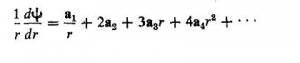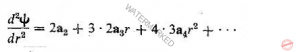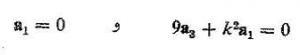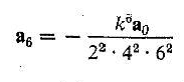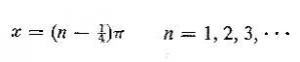مبانی آکوستیک
ارتعاش پوسته های گرد و ورقه ها
بخش دوم معادله موج برای يك پوسته گرد. در حل معادله موج برای ارتعاش عرضي يك پوسته، یکی از کارهای اساسی به کار بردن سیستم مختصات فضایی خاصی است که شکل مرزی پوسته در آن به صورتی ساده بیان گردد. همانطور که مشاهده کردیم، به کار بردن سیستم مختصات دکارتی برای يك پوسته چهارگوش بحث آن را آسان کرد. به همین شکل، مختصات قطبی نیز بحث يك پوست گرد را آسان می سازد. متأسفانه بعلت محدود بودن تعداد سیستمهای مختصات، تعداد پوسته های قابل حل نیز محدود می گردد. معادله 4.2 را می توان در حالت عمومی، که مناسب برای هر سیستم مختصات می باشد به صورت زیر نوشت
که در آن ![]() ، اوپراتور دو بعدی لاپلاس، به جای عبارت
، اوپراتور دو بعدی لاپلاس، به جای عبارت ![]() قرار گرفته است. برای يك پوسته گرد که دارای مرزی ثابت به شعاع a است، باید اوپراتور لاپلاس را در مختصات قطبی، r و
قرار گرفته است. برای يك پوسته گرد که دارای مرزی ثابت به شعاع a است، باید اوپراتور لاپلاس را در مختصات قطبی، r و ![]() نوشت که در آن
نوشت که در آن ![]() و
و ![]() است. با مشتق گیری جزئی نسبت به r و
است. با مشتق گیری جزئی نسبت به r و ![]() ، و در نظر گرفتن اینکه r و
، و در نظر گرفتن اینکه r و ![]() توابعی ضمنی از x و z هستند، لاپلاسین در مختصات قطبی چنین به دست می آید
توابعی ضمنی از x و z هستند، لاپلاسین در مختصات قطبی چنین به دست می آید
با قراردادن این رابطه در معادله خواهیم داشت
که يك حالت بسیار عمومی از معادله موج است و برای بحث ارتعاشهای عرضی بسیار مناسب است. تقریبا در تمام حالات عملی که در آکوستيك قابل اهمیت است، پوسته با يك تقارن دایروی ارتعاش می کند، یعنی ![]() و تو و تابعی از مختصات سمتی
و تو و تابعی از مختصات سمتی ![]() نیست. در این حالت، معادله
نیست. در این حالت، معادله ![]() به صورت ساده زیر در می آید
به صورت ساده زیر در می آید
و فقط حل آن بعد، مورد بررسی قرار خواهد گرفت. ارتعاشهای متقارن آزاد در پوسته گرد . مانند ارتعاشهای عرضی میله، حل معادله 4.5b را می توان به راحتی با فرض اینکه تغییر مکان را می توان از حاصلضرب دوجمله که یکی بستگی به زمان و دیگری بستگی به مکان دارد، به دست آورد. بدین معنی که برای ارتعاشهای هارمونيك، فرض کنیم
که در آن ![]() يك تابع فقط از ۶ است. با قراردادن معادله 4.7 در معادله 4.5b معادله اخیر به این صورت در می آید
يك تابع فقط از ۶ است. با قراردادن معادله 4.7 در معادله 4.5b معادله اخیر به این صورت در می آید
که در آن
برای حل معادله 4.8 فرض می کنیم که حل آن يك سری به صورت زیر باشد
پس
و
پس از قراردادن این عبارتها در معادله 4.8 خواهیم داشت
چون برای تمام مقادير r این جمع باید صفر باشد، هر ضریبی که در يك توانی از r ضرب شده است باید صفر باشد، پس
بنا بر این، ![]() . به همین ترتیب، تمام ثابتهای فرد دیگر
. به همین ترتیب، تمام ثابتهای فرد دیگر ![]() و
و ![]() غیره … را می توان نشان داد که برابر صفر هستند. ولی برای ثابتهای به شماره زوج داریم
غیره … را می توان نشان داد که برابر صفر هستند. ولی برای ثابتهای به شماره زوج داریم
و
به همین ترتیبت
و غیره …………….. پس حل سری معادله ی 4.8 چنین خواهد شد
سری داخل کروشه تابع مشهور مرتبه صفر بسلا از نوع اول است، که معمولا به صورت ![]() نوشته می شود. مقادیر تابع
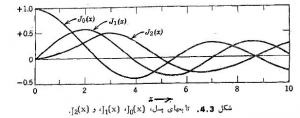
نوشته می شود. مقادیر تابع ![]() ، همراه با تابعهای قابل استفاده بسل، در جدول III ضمیمه آورده شده ، همچنين
، همراه با تابعهای قابل استفاده بسل، در جدول III ضمیمه آورده شده ، همچنين ![]() و در شکل 4.3 ترسیم گردیده است. تابع
و در شکل 4.3 ترسیم گردیده است. تابع
حل كامل معادله 4.8 نیست، چون این معادله يك معادله دیفرانسیل مرتبه دوم است و حل آن باید دو ثابت اختیاری داشته باشد. می توان نشان داد که حل دیگری به صورت ![]() که
که ![]() وجود دارد که در آن
وجود دارد که در آن ![]() تابع بسل مرتبه ی صفر از نوع دوم است. ولی چون
تابع بسل مرتبه ی صفر از نوع دوم است. ولی چون ![]() در
در ![]() بینهایت می شود، و این شرط را که تغيير مكان باید مقادير كوچك داشته باشد تامین نمی کند، بنابراین باید
بینهایت می شود، و این شرط را که تغيير مكان باید مقادير كوچك داشته باشد تامین نمی کند، بنابراین باید ![]() باشد معادلة بسل. معادله 4.8 حالت خاصی از معادله دیفرانسیل بسل، یعنی
باشد معادلة بسل. معادله 4.8 حالت خاصی از معادله دیفرانسیل بسل، یعنی
است . معادله ی 4.12 هنگامی که به جای y تابع ![]() ، و به جای x مقدار kr، و به جای m صفر قرار دهیم به معادله 4.8 تبدیل می گردد. اگر در معادله 4.12، m يك عدد صحیح غير از صفر باشد، حل آن تابع بسل دیگری خواهد بود، که به نام تابع بسل نوع اول از مرتبه m خوانده می شود و با
، و به جای x مقدار kr، و به جای m صفر قرار دهیم به معادله 4.8 تبدیل می گردد. اگر در معادله 4.12، m يك عدد صحیح غير از صفر باشد، حل آن تابع بسل دیگری خواهد بود، که به نام تابع بسل نوع اول از مرتبه m خوانده می شود و با ![]() نشان داده می شود. در این کتاب فقط تابعهای
نشان داده می شود. در این کتاب فقط تابعهای ![]() و
و ![]() مورد استفاده قرار خواهند گرفت ، و رسم آنها همراه با
مورد استفاده قرار خواهند گرفت ، و رسم آنها همراه با ![]() در شکل 4.3 نشان داده شده است. در این شکل مشاهده می شود که تابع بسل
در شکل 4.3 نشان داده شده است. در این شکل مشاهده می شود که تابع بسل ![]() شبيه يك تابع کسینوس میراست در حالیکه
شبيه يك تابع کسینوس میراست در حالیکه ![]() و
و ![]() به يك تابع سینوس ميرا شباهت دارند.
به يك تابع سینوس ميرا شباهت دارند.
مقدارهایی از x که به ازای آنها تابع ![]() صفر می شود چنین هستند
صفر می شود چنین هستند
که می توان آنها را به صورت زیر هم نوشت
یا تقريبا
بعضی از روابط و خواص توابع بسل در جدول خواننده می تواند به متنیهای مربوط به «تابعهای بسهل» رجوع کند.